Question

如图，已知AC∥BD，EA、EB分别平分∠CAB和∠DBA，CD过点E，则AB与AC+BD相等吗？请说明理由．

Answer 1

分析：在AB上截取AC=AF，连接EF，根据SAS证△CAE≌△FAE，推出∠C=∠AFE，求出∠D=∠EFB，根据AAS证△BEF≌△BED，推出BF=BD即可．

解答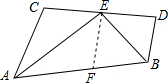：解：AB=AC+BD，
理由是：在AB上截取AC=AF，连接EF，
∵AE平分∠CAB，
∴∠CAE=∠BAE，
∵在△CAE和△FAE中

AC=AF ∠CAE=∠FAE AE=AE

，
∴△CAE≌△FAE（SAS），
∴∠C=∠AFE，
∵AC∥BD，
∴∠C+∠D=180°，
∵∠EFB+∠AFE=180°，
∴∠D=∠EFB，
∵BE平分∠ABD，
∴∠DBE=∠FBE，
∵在△BEF和△BED中

∠D=∠EFB ∠FBE=∠DBE BE=BE

，
∴△BEF≌△BED（AAS），
∴BF=BD，
∵AB=AF+BF，AC=AF，BF=BD
∴AB=AC+BD．

点评：本题考查了全等三角形的性质和判定，平行线的性质，角平分线性质等知识点，全等三角形的对应边相等，对应角相等，注意证明此类型题的证明方法．