Question

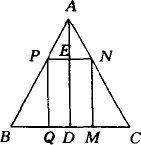
如图所示，在生产中，为了节约原材料，加工零件时常用一些边角余料，△ABC为锐角三角形废料．其中BC＝12 cm，BC边上高AD＝8 cm，在△ABC上截取矩形PQMN，与BC边重合，画出草图说明P，N两点落在什么位置上，才能使它的面积最大？最大面积是多少？并求出这时矩形的长和宽．

Answer 1

解析：

[答案]如图，设PN交AD于E．PQ长为x(cm)，PN长为y cm．矩形的面积为S(cm2)．则AE＝(8－x)cm， 　　∵PN∥BC．∴∠APN＝∠ABC． 　　又∠PAN＝∠BAC，∴△APN∽△ABC．∴＝， 　　即＝．∴y＝(8－x)． 　　∴S＝PN·PQ＝xy＝(8－x)x＝－x2＋12x(0＜x＜8)． 　　即S＝－(x－4)2＋24． 　　∴当x＝4时，S有最大值24，此时y＝×(8－4)＝6cm． 　　此时＝＝＝＝，即P是AB的中点，Q是BD的中点． 　　故当P，Q分别为AB，BD的中点时，才可使矩形PQMN的面积最大，最大面积为24cm2，此时矩形的长为6cm，宽为4cm．