题目内容
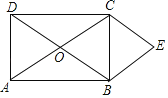
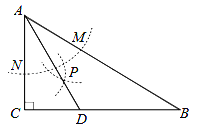
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交![]() 、
、![]() 于点
于点![]() 和
和![]() ,再分别以
,再分别以![]() 、
、![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,则下列说法中正确的个数是( )
,则下列说法中正确的个数是( )
①![]() 是
是![]() 的平分线;②
的平分线;②![]() ;③
;③![]() ;④
;④![]()
A.1B.2C.3D.4
【答案】C
【解析】
①连接NP,MP,根据SSS定理可得△ANP≌△AMP,故可得出结论;
②先根据三角形内角和定理求出∠CAB的度数,再由AD是∠BAC的平分线得出∠1=∠2=30°,
根据直角三角形的性质可知∠ADC=60°;
③根据∠1=∠B可知AD=BD,故可得出结论;
④先根据直角三角形的性质得出∠2=30°,CD=![]() AD,再由三角形的面积公式即可得出结论.
AD,再由三角形的面积公式即可得出结论.
①证明:连接NP,MP,

在△ANP与△AMP中,
∵ ,
,
∴△ANP≌△AMP,
则∠CAD=∠BAD,
故AD是∠BAC的平分线,故此选项正确;
②证明:∵在△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°.
∵AD是∠BAC的平分线,
∴∠1=∠2=![]() ∠CAB=30°,
∠CAB=30°,
∴∠3=90°∠2=60°,∠ADC=60°,故此选项正确;
③证明:∵∠1=∠B=30°,
∴AD=BD,故此选项正确;
④证明:∵在Rt△ACD中,∠2=30°,
∴CD=![]() AD,
AD,
∴BC=BD+CD=AD+![]() AD=
AD=![]() AD,
AD,![]() =
=![]() ACCD=
ACCD=![]() ACAD,
ACAD,
∴![]() =
=![]() ACBC=
ACBC=![]() AC
AC![]() AD=
AD=![]() ACAD,
ACAD,
∴![]() =1:3,故此选项不正确;
=1:3,故此选项不正确;
故选C.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目