题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=30cm,AC=40cm,点D在线段AB上从点B出发,以2cm/s的速度向终点A运动,设点D的运动时间为t.
(1)AB= cm,AB边上的高为 cm;
(2)点D在运动过程中,当△BCD为等腰三角形时,求t的值.

【答案】(1)50,24;(2)15,18,12.5.
【解析】
试题分析:(1)在![]() 中,由勾股定理即可求出AB,由直角三角形的面积即可求出斜边上的高;
中,由勾股定理即可求出AB,由直角三角形的面积即可求出斜边上的高;
(2)分三种情况:当![]() 时,得出
时,得出![]() ,即可得出结果;当
,即可得出结果;当![]() 时,作
时,作![]() 于
于![]() ,则
,则![]() ,由(1)得出
,由(1)得出![]() ,由勾股定理求出BE,即可得出结果;当
,由勾股定理求出BE,即可得出结果;当![]() 时,
时,![]() ,证明
,证明![]() ,得出
,得出![]() ,即可得出结果.
,即可得出结果.
试题解析:(1)在![]() 中,
中,![]()
![]()
![]()
![]()
![]() 作
作![]() 边上的高
边上的高![]() ,如图1所示:
,如图1所示:![]()
![]()
![]()
分三种情况:当![]() 时,得出img src="https://thumb.zyjl.cn/questionBank/Upload/2017/12/28/21/6863cad7/SYS201712282104021498685941_DA/SYS201712282104021498685941_DA.025.png" width="51" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,
时,得出img src="https://thumb.zyjl.cn/questionBank/Upload/2017/12/28/21/6863cad7/SYS201712282104021498685941_DA/SYS201712282104021498685941_DA.025.png" width="51" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,![]() ;当
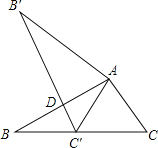
;当![]() 时,作
时,作![]() 于
于![]() ,如图2所示,则
,如图2所示,则![]() ,由(1)得出
,由(1)得出![]() ,在
,在![]() 中,由勾股定理得:
中,由勾股定理得:![]()
![]() ;当
;当![]() 时,
时,![]() ,
,
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()



练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目