题目内容

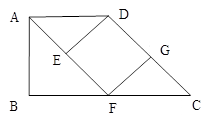
（本题10分）如图，梯形ABCD中，AD∥BC，BC=2AD，F、G分别为边BC、CD的中点，连接AF，FG，过D作DE∥GF交AF于点E。

（1）证明△AED≌△CGF

（2）若梯形ABCD为直角梯形，判断四边形DEFG是什么特殊四边形？并证明你的结论。

 

 


 

 

 

 

 

（1）证明；∵ BC=2AD、点F为BC中点

∴CF=AD 

∵AD∥CF  ∴四边形AFCD为平行四边形

∴∠FAD=∠C　　

∵DE∥FG  ∴∠DEA=∠AFG

∵AF∥CD   ∴∠AFG=∠FGC 

∴∠DEA=∠FGC  ．

∴△AED≌△CGF　

（2）连结DF

易证四边形ADCF是平行四边形，四边形ABFD是矩形．

又因为点E,G分别为AF,CD的中点

所以DE=EF=FG=GD 即四边形DEFG是菱形。

解析:略

 

练习册系列答案
相关题目

（本题10分）如图，直线x－2y=－5和x+y=1分别与x轴交于A、B两点，这两条线的交点为P．

1.(1)求点P的坐标．    

2.(2)求△APB的面积．  

 

（本题10分）如图，P是双曲线的一个分支上的一点，以点P为圆心，1个单位长度为半径作⊙P，设点P的坐标为（，）．

（1）求当为何值时，⊙P与直线相切，并求点P的坐标．

（2）直接写出当为何值时，⊙P与直线相交、相离．

 

 

（本题10分）如图，以点M（－1,0）为圆心的圆与y轴、x轴分别交于点A、B、C、D，直线y＝－ x－ 与⊙M相切于点H，交x轴于点E，交y轴于点F．

   1.（1）请直接写出OE、⊙M的半径r、CH的长；（3分）

2.（2）如图1，弦HQ交x轴于点P，且DP:PH＝3:2，求COS∠QHC的值；（3分）

3.（3）如图2，点K为线段EC上一动点（不与E、C重合），连接BK交⊙M于点T，弦AT交x轴于点N．是否存在一个常数a，始终满足MN·MK＝a，如果存在，请求出a的值；如果不存在，请说明理由．（3分）

       

 

 

 

 

 

 

 

 

 

 

 

 

（本题10分）如图，在Rt△ABC中，∠C＝90°，点O在AB上，以O为圆心，OA长为半径的圆与AC、AB分别交于点D、E，且∠CBD＝∠A．
试判断直线BD与⊙O的位置关系，并证明你的结论．

 

（本题10分）如图4，边长为的矩形，它的周长为14，面积为10，求下列各式的值：(1)   (2)

 

 

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网