Question

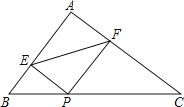
【题目】如图，将平行四边形ABCD的边DC延长至点E ， 使CE＝DC ， 连接AE ， 交BC于点F ．

（1）求证：△ABF≌△ECF；
（2）连接AC、BE ， 则当∠AFC与∠D满足什么条件时，四边形ABEC是矩形？请说明理由

Answer 1

【答案】
（1）

解答：证明：在平行四边形ABCD中，AB∥CD，AB＝CD，

∴∠BAE＝∠AEC，又∵CE＝CD，

∴AB＝CE，在△ABF和△ECF中， ，

∴△ABF≌△ECF（AAS）．

（2）

解答：解：当∠AFC＝2∠D时，四边形ABEC是矩形，理由如下：

∵四边形ABCD是平行四边形，

∴BC∥AD，AB∥DC，AB＝DC，

∴∠BCE＝∠D，AB∥EC，

又∵CE＝DC，

∴四边形ABEC是平行四边形，

∵∠AFC＝∠FEC＋∠BCE，

∴当∠AFC＝2∠D时，则有∠FEC＝∠FCE，

∴FC＝FE，

∴四边形ABEC是矩形．

【解析】（1）由四边形ABCD是平行四边形，CE＝DC ， 易证得∠ABF＝∠ECF ， ∠AFB＝∠EFC ， AB＝EC ， 则可证得△ABF≌△ECF；（2）首先根据四边形ABCD是平行四边形，得到四边形ABEC是平行四边形，然后证得FC＝FE ， 利用对角线互相相等的四边形是矩形判定四边形ABEC是矩形．
【考点精析】认真审题，首先需要了解平行四边形的性质(平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分)，还要掌握矩形的判定方法(有一个角是直角的平行四边形叫做矩形；有三个角是直角的四边形是矩形；两条对角线相等的平行四边形是矩形)的相关知识才是答题的关键．