Question

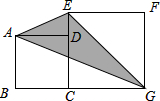已知如图，在线段BG同侧作正方形ABCD和正方形CEFG，其中BG=10，BC：CG=2：3，则S_△ECG=

18

，S_△AEG=

18

．

Answer 1

分析：求出BC，CG，根据三角形面积公式和矩形的面积公式求出即可．

解答：解：
∵BG=10，BC：CG=2：3，
∴BC=4，CG=6，
∵四边形ABCD和四边形EFGC是正方形，
∴BC=AB=4，FG=EF=CG=6，
延长FE和BA交于N，
∵四边形ABCD和四边形EFGC是正方形，
∴∠NED=∠EDA=∠DAN=90°，
∴四边形BNFG是矩形，
∴EN=BC=4，NF=BG=10，BN=CF=6，
∴S_△ECG=

1

2

×CG×FG=

1

2

×6×6=18，
S_△AEG=S_矩形NBGF-S_△ABG-S_△EFG-S_△ANE
=10×6-

1

2

×4×10-

1

2

×6×6-

1

2

×（6-4）×4=18，
故答案为：18，18．

点评：本题考查了正方形性质，矩形性质，三角形面积的应用，主要考查学生的计算能力．