题目内容
 工程上常用钢珠来测量零件上小孔的直径,假设钢珠的直径是12毫米,测得钢珠顶端离零件表面的距离为9毫米,如图所示,则这个小孔的直径AB是多少毫米?
工程上常用钢珠来测量零件上小孔的直径,假设钢珠的直径是12毫米,测得钢珠顶端离零件表面的距离为9毫米,如图所示,则这个小孔的直径AB是多少毫米?
分析:设钢珠的圆心为O,过O作OC⊥AB于C,交优弧AB于D,连OC,则OA=12÷2=6mm,CD=9mm,OC=9mm-6mm=3mm,根据垂径定理得到CA=CB,在Rt△AOC中,利用勾股定理可计算出AC,即可得到这个小孔的直径AB.
解答: 解:如图,
解:如图,
设钢珠的圆心为O,过O作OC⊥AB于C,交优弧AB于D,连OC,
则OA=12÷2=6mm,CD=9mm,OC=9mm-6mm=3mm,
∵OC⊥AB,
∴CA=CB,
在Rt△AOC中,AC=
=
=3
,
∴AB=6
mm.
所以这个小孔的直径AB是6
毫米.
 解:如图,
解:如图,设钢珠的圆心为O,过O作OC⊥AB于C,交优弧AB于D,连OC,
则OA=12÷2=6mm,CD=9mm,OC=9mm-6mm=3mm,
∵OC⊥AB,
∴CA=CB,
在Rt△AOC中,AC=
| OA2-OC2 |
| 62-32 |
| 3 |
∴AB=6
| 3 |
所以这个小孔的直径AB是6
| 3 |
点评:本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
 工程上常用钢珠来测量零件上小孔的直径,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小孔的直径AB是
工程上常用钢珠来测量零件上小孔的直径,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小孔的直径AB是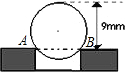 如图,工程上常用钢珠来测量零件上小孔的直径,假设钢珠的直径是12毫米,测得钢珠顶端离零件表面的距离为9毫米,则这个小孔的直径AB是
如图,工程上常用钢珠来测量零件上小孔的直径,假设钢珠的直径是12毫米,测得钢珠顶端离零件表面的距离为9毫米,则这个小孔的直径AB是 如图,工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10cm,测得钢珠顶端离零件表面的距离为8cm,则这个小圆孔的宽口AB的长度为多少?
如图,工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10cm,测得钢珠顶端离零件表面的距离为8cm,则这个小圆孔的宽口AB的长度为多少? 工程上常用钢珠来测量零件上小孔的直径,假设钢珠的直径是10㎜,测得钢珠顶端离零件表面的距离为8㎜,如图所示,求这个小孔的直径AB的长.
工程上常用钢珠来测量零件上小孔的直径,假设钢珠的直径是10㎜,测得钢珠顶端离零件表面的距离为8㎜,如图所示,求这个小孔的直径AB的长.