Question

【题目】如图，已知楼房旁边有一池塘，池塘中有一电线杆高米，在池塘边处测得电线杆顶端的仰角为，楼房顶点的仰角为，又在池塘对面的处，观测到，，在同一直线上时，测得电线杆顶端

的仰角为． (注:tan75=2+)

（1）求池塘边，两点之间的距离；

（2）求楼房的高．

Answer 1

【答案】间的距离为米，楼房的高为米．

【解析】

(1)分别解Rt△ABE与Rt△BEF,可得AB与BF的大小.由AF=AB+BF可得结果;

(2)设CD=x.在Rt△FCD中,可得CF的值,根据相似三角形的性质,可得比例关系求解.

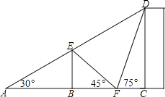
解:如图：

(1)在Rt△ABE中,

∠A=30,BE=10,

= AB=10,

在Rt△EBF中,

∠BFE=45,

BF=BE=10,

AF=10+10;

(2)BE=10,∠A=30,AB=10,

设CD=x.则CF==.

∠EBA=∠DCA=90,∠A=30,

△ABE~△ACD,

由相似三角形的性质可得:,

即,

解得x=10+5.

答:AF间的距离为(10+10)米,楼房CD的高为(10+5)米.