题目内容
如图,在矩形 中,把点
中,把点 沿
沿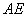 对折,使点
对折,使点 落在
落在 上的
上的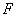 点,已知
点,已知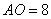 。
。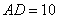 .
.
(1)求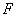 点的坐标;
点的坐标;
(2)如果一条不与抛物线对称轴平行的直线与该抛物线仅有一个交点,我们把这条直线称为抛物线的切线,已知抛物线经过点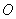 ,
,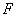 ,且直线
,且直线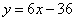 是该抛物线的切线,求抛物线的解析式;
是该抛物线的切线,求抛物线的解析式;
(3)直线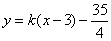 与(2)中的抛物线交于
与(2)中的抛物线交于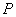 、
、 两点,点
两点,点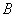 的坐标为
的坐标为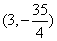 ,求证:
,求证: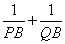 为定值(参考公式:在平面直角坐标系中,若
为定值(参考公式:在平面直角坐标系中,若 ,
,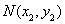 ,则
,则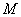 ,
,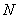 两点间的距离为
两点间的距离为 )
)
 |
解:(1)由 ≌
≌  得
得

又由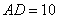 ,
,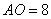
∴ ,
,
∴
(2)依题意可设过点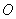 、
、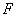 的抛物线解析式为
的抛物线解析式为
依题意知,抛物线与直线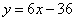 相切,
相切,
即由 得
得 有两个相等的实数根
有两个相等的实数根
∴ ,得
,得
∴抛物线的解析式为 
(3)设 ,
, 假设
假设 ,
, 依题意得
依题意得
 得
得
∴ ,
,
又 ,
,
∵



 即
即

 为定值
为定值
 |

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
在一次中学生田径运动会上,参加调高的15名运动员的成绩如下表所示:
| 成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 1 | 2 | 4 | 3 | 3 | 2 |
那么这些运动员跳高成绩的众数是( )
A.4 B.1.75 C.1.70 D.1.65
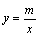 与直线
与直线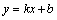 相交于点M,N,且点M的坐标为(1,3),点N的纵坐标为
相交于点M,N,且点M的坐标为(1,3),点N的纵坐标为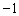 .根据图象信息可得关于x的方程
.根据图象信息可得关于x的方程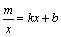 的解为( )
的解为( )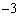 ,1 B.
,1 B.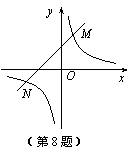
 平方米,预计到明年年底的绿化面积将会增加到
平方米,预计到明年年底的绿化面积将会增加到 平方米,求这两年的年平均增长率。
平方米,求这两年的年平均增长率。 ,且
,且 ,垂足为
,垂足为 ,则
,则 .
.

