Question

【题目】综合与探究

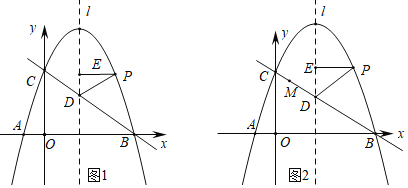
如图1，在平面直角坐标系中，抛物线y＝ax2+x+3与x轴交于A，B两点（A在B左侧），与y轴交于点C．点A坐标为（﹣1，0）．直线l为该抛物线的对称轴，且交直线BC于点D．抛物线上有一动点P，且横坐标为m（4＜m＜9），连接PD，过点P作PE⊥l于点E．

（1）求抛物线及直线BC的函数表达式．

（2）当△DEP与△BOC相似时，求m的值；

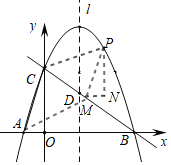
（3）如图2，点M为直线BC上一动点，是否存在点P，使得以点A，C，P．M为顶点的四边形是平行四边形？若存在，直接写出此时点P和点M的坐标；若不存在，说明理由．

Answer 1

【答案】（1）y＝－ x+3，y＝﹣x2+x+3；（2）m的值为 或8；（3）存在点P坐标为（，），点M坐标为（ ）

【解析】

（1）将点A坐标代入可求抛物线解析式，求出B、C坐标，待定系数法求出直线BC的解析式

（2）分类讨论相似关系，当△DEP～△COB和当△DEP～ABOC时，找好边角的对应关系，可求m的值．

（3）因为点P的坐标范围要求，所以点P只存在一种情况，利用全等关系，解方程等量关系获得点M和P点坐标．

（1）把点A（﹣1，0）代入y＝ax2+x+3中，得a＝﹣∴抛物线的函数表达式为，y＝﹣x2+x+3

当x＝0，得y＝3，∴点C的坐标为（0，3）

当y＝0时，得﹣y＝﹣x2+x+3＝0

解，得x1＝﹣1，x2＝9．∵点A在点B左侧点B坐标为（9，0）

设直线BC的函数表达式为y＝kx+b，

把点B（9，0）和C（0，3）代入上式，

得 解得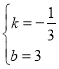 ∴直线BC的函数表达式为y＝－x+3；

（2）在Rt△BOC中，OB＝9，OC＝3，∵PE⊥l于点E．∠PED＝∠BOC＝90°．

∵直线l为抛物线y＝﹣x2+x+3的对称轴，

∴直线l为x＝﹣＝﹣÷[2×（﹣）]＝4

∴点D和E的横坐标为4

把x＝4代入y＝-x+3中，得y＝-x4+3＝．

∴点D坐标为（4，）

∵点P是抛物线上的点，

∴设P（m，﹣m2+m+3），E（4，﹣m2+m+3）

∵4＜m＜9，且△DEP与△BOC相似

∴点E在点D上方，点P在点E右侧．

∴DE＝﹣m2+m+3﹣＝﹣m2+m+，PE＝m﹣4

①当△DEP～ABOC时，＝，

即＝

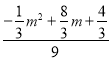
解得m1＝，m2＝（舍）

②当△DEP～△COB时，＝，

即＝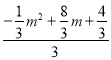

解得m1＝8，m2＝﹣1（舍）

∴当△DEP与△BOC相似时，m的值为 或8；

（3）∵点P的横坐标在4与9之间

∴A、C、P、M组成的平行四边形只有一种情况，如图

可证△PMN≌△ACO（AAS）

∴OA＝MN＝1，PN＝CO＝3

设点M（m，-m+3）

则P（m+1，-m+3+3）

将点P坐标代入解析式，可解得m＝

∴存在点P坐标为（，），点M坐标为（）.