题目内容
材料:结合具体的数,通过特例探究当a>0时,a与 的大小.
的大小.
解:当a>1时,取a=2,则2> ; 取a=
; 取a= ,则
,则 >
> ;…,所以a>
;…,所以a> .
.
当a=1时,a= .
.
当0<a<1时,取a= ,则
,则 <2;取a=
<2;取a= ,则
,则 <
< ;…,所以a<
;…,所以a< .
.
综上,当a>1时,a> ;当a=1时,a=
;当a=1时,a= ;当0<a<1时,a<
;当0<a<1时,a< .
.
问题:结合具体的数,通过特例探究当a<0时,a与 的大小.
的大小.
解:当0>a>-1时,取a=- ,则-2<-
,则-2<- ; 取a=-
; 取a=- ,则-3
,则-3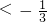 ;…,所以a>
;…,所以a> .
.
当a=-1时,a= .
.
当a<-1时,取a=-3,则- >-3;取a=-4,则-
>-3;取a=-4,则-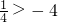 ;…,所以a<
;…,所以a< .
.
综上,当-1<a<0时,a> ;当a=1时,a=
;当a=1时,a= ;当a>-1时,a<
;当a>-1时,a< .
.
分析:解决该题,结合-1为例子,分别从大于,等于,小于进行考虑,后综述.
点评:本题考查了有理数的大小比较,以例子进行类推,首先找到适合的界数,难度一般.
 ,则-2<-
,则-2<- ; 取a=-
; 取a=- ,则-3
,则-3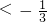 ;…,所以a>
;…,所以a> .
.当a=-1时,a=
 .
.当a<-1时,取a=-3,则-
 >-3;取a=-4,则-
>-3;取a=-4,则-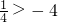 ;…,所以a<
;…,所以a< .
.综上,当-1<a<0时,a>
 ;当a=1时,a=
;当a=1时,a= ;当a>-1时,a<
;当a>-1时,a< .
.分析:解决该题,结合-1为例子,分别从大于,等于,小于进行考虑,后综述.
点评:本题考查了有理数的大小比较,以例子进行类推,首先找到适合的界数,难度一般.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目