题目内容
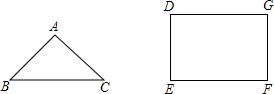
等腰直角三角形各边中点连线围成的多边形是
- A.平行四边形
- B.等腰三角形
- C.等腰直角三角形
- D.等边三角形
C
分析:根据三角形的中位线平行于第三边并且等于第三边的一半可得新三角形的三边与原三角形的三边对应成比例,从而判断两三角形相似,即可得解.
解答: 解:如图,∵D、E、F是AB、BC、AC的中点,
解:如图,∵D、E、F是AB、BC、AC的中点,
∵DE= AC,EF=
AC,EF= AB,DF=
AB,DF= BC,
BC,
∴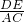 =
= =
=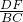 =
= ,
,
∴△EFD∽△ABC,
∵△ABC是等腰直角三角形,
∴△EFD是等腰直角三角形.
故选C.
点评:本题考查了等腰直角三角形的判定,三角形的中位线平行于第三边并且等于第三边的一半的性质,判断出两三角形相似是解题的关键.
分析:根据三角形的中位线平行于第三边并且等于第三边的一半可得新三角形的三边与原三角形的三边对应成比例,从而判断两三角形相似,即可得解.
解答:
 解:如图,∵D、E、F是AB、BC、AC的中点,
解:如图,∵D、E、F是AB、BC、AC的中点,∵DE=
 AC,EF=
AC,EF= AB,DF=
AB,DF= BC,
BC,∴
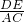 =
= =
=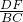 =
= ,
,∴△EFD∽△ABC,
∵△ABC是等腰直角三角形,
∴△EFD是等腰直角三角形.
故选C.
点评:本题考查了等腰直角三角形的判定,三角形的中位线平行于第三边并且等于第三边的一半的性质,判断出两三角形相似是解题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目