题目内容
如图，大楼高30m，远处有一塔BC，小明在楼底A处，测得塔顶的仰角为60°，爬到楼顶测得塔顶的仰角为30°．根据以上数据，你能求出塔高BC吗？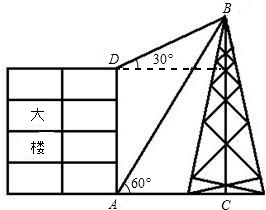
分析：易得CE=AD，设BE为未知数，利用30°的正切值可求得DE，也就是AC的长，然后利用60°的正切值即可求得BE长，加上30即为塔高．
解答：
解：作DE⊥BC交BC于点E，
设BE为x．
∴∠DEB=∠DEC=90°，
∵∠BCA=90°，
∴四边形ACED是矩形．
∴DE=
=
x，
∴AC=DE=
x，
∵tan60°=
∴
=
，
解得x=15，
∴塔高为15+30=45米．
答：塔高BC为45米．
解：作DE⊥BC交BC于点E，设BE为x．
∴∠DEB=∠DEC=90°，
∵∠BCA=90°，
∴四边形ACED是矩形．
∴DE=
| BE |
| tan30° |
| 3 |
∴AC=DE=
| 3 |
∵tan60°=
| BE+EC |
| AC |
∴
| 3 |
| x+30 | ||
|
解得x=15，
∴塔高为15+30=45米．
答：塔高BC为45米．
点评：考查仰角的定义，能借助仰角构造直角三角形并解直角三角形是仰角问题常用的方法．
练习册系列答案
应用题作业本系列答案
相关题目
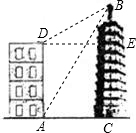如图，大楼高30m，附近有一座塔BC，某人在楼底A处测得塔顶的仰角为60°，爬到楼顶D处测得塔顶的仰角为30°，求塔高BC及大楼与塔之间的距离AC（结果精确到0.01m，参考数据：
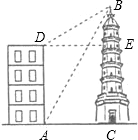如图，大楼高30m，远处有一塔BC，某人在楼底A处测得塔顶的仰角为60°，爬到楼顶D测得塔顶的仰角为30°．则塔高BC为
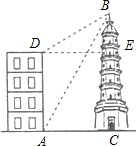如图，大楼高30m，远处有一塔BC，某人在楼底A处测得塔顶的仰角为60°，爬到楼顶D测得塔顶的仰角为30°．求：