题目内容
如图:等边△PQR,∠APB=120°,AP= ,AQ=4,PB=
,AQ=4,PB= ,则RQ的长为 ,△PRB的面积为 .
,则RQ的长为 ,△PRB的面积为 .
【答案】分析:根据已知条件,只要证得△PAQ∽△BPR,就可得:PA:BP=AQ:PR,则可算出PR、BR的长,在等边△PQR中,PR=RQ,可求出它的高,也就是△PRB的高,由此面积也可求.
解答:解:∵∠QPR=∠PQR=∠PRQ=60°
∴∠PQA=∠PRB=120°
∵∠APB=120°
∴∠APQ+∠BPR=∠APB-∠QPR=120°-60°=60°
∵在△APQ中,∠A+∠APQ=180°-∠AQP=60°
∴∠A=∠BPR
∴△PAQ∽△BPR
∴PA:BP=AQ:PR
即2 :
: =4:PR
=4:PR
∴PR=2
在等边△PQR中,PQ=RQ=PR=2 ,底边RQ的高为
,底边RQ的高为 =
=
∴PQ:BR=AQ:PR,即2 :BR=4:2
:BR=4:2 ,BR=2
,BR=2
∵△PRB的高为等边△PQR的高
∴△PRB的面积为 ×2×
×2× =
= .
.
点评:该题主要考查了相似三角形的判定及性质,及三角形面积的求法,注意对应边之比.
解答:解:∵∠QPR=∠PQR=∠PRQ=60°
∴∠PQA=∠PRB=120°
∵∠APB=120°
∴∠APQ+∠BPR=∠APB-∠QPR=120°-60°=60°
∵在△APQ中,∠A+∠APQ=180°-∠AQP=60°
∴∠A=∠BPR
∴△PAQ∽△BPR
∴PA:BP=AQ:PR
即2
 :
: =4:PR
=4:PR∴PR=2

在等边△PQR中,PQ=RQ=PR=2
 ,底边RQ的高为
,底边RQ的高为 =
=
∴PQ:BR=AQ:PR,即2
 :BR=4:2
:BR=4:2 ,BR=2
,BR=2∵△PRB的高为等边△PQR的高
∴△PRB的面积为
 ×2×
×2× =
= .
.点评:该题主要考查了相似三角形的判定及性质,及三角形面积的求法,注意对应边之比.

练习册系列答案
相关题目
 如图:等边△PQR,∠APB=120°,AP=
如图:等边△PQR,∠APB=120°,AP=
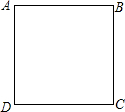
 如图:等边△PQR,∠APB=120°,AP=
如图:等边△PQR,∠APB=120°,AP= ,AQ=4,PB=
,AQ=4,PB= ,则RQ的长为________,△PRB的面积为________.
,则RQ的长为________,△PRB的面积为________.