ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΉέΚœ”κ ΒΦυ
Έ Χβ«ιΨ≥ΘΚ
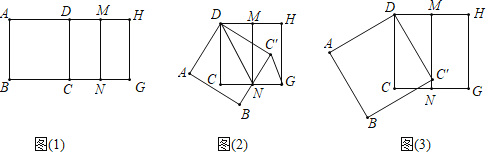
ΐ―ßΩΈ…œΘ§άœ Π»ΟΆ§―ßΟ«ΡΟΝΫ’≈¥σ–ΓœύΆ§ΒΡ’ΐΖΫ–Έ÷ΫΤ§Ήω–ΐΉΣΧΫΨΩΜνΕ·Θ§≤ΔΧα≥ω ΐ―ßΈ ΧβΦ”“‘ΫβΨωΘΚ»γΆΦΘ®1Θ©Θ§ΥΡ±Ώ–ΈABCDΚΆDCGHΕΦ «’ΐΖΫ–ΈΘ§ΒψMΘ§NΖ÷±π «DHΘ§CGΒΡ÷–ΒψΘ§ΫΪ’ΐΖΫ–ΈABCD“‘ΒψDΈΣ÷––ΡΘ§Ρφ ±’κ–ΐΉΣΫ«Ε»ΠΝΘ®0ΘΦΠΝΘΦ90ΓψΘ©Θ§ΒΟΒΫ’ΐΖΫ–ΈABC'DΘ°
ΫβΨωΈ ΧβΘΚ
œ¬Οφ «–Υ»Λ–ΓΉιΧα≥ωΝΫΗω ΐ―ßΈ ΧβΘ§«κΡψΫβΨω’β–©Έ ΧβΘ°
Θ®1Θ©»γΆΦΘ®2Θ©Θ°Β±±ΏBC'’ΐΚΟΨ≠ΙΐΒψN ±Θ°–¥≥ωœΏΕΈC'GΚΆDNΒΡΈΜ÷ΟΙΊœΒΘ§≤Δ÷ΛΟς
Θ®2Θ©»γΆΦΘ®3Θ©Θ§Β±ΒψCΓδ’ΐΚΟ¬δ‘ΎMN…œ ±Θ§«σ–ΐΉΣΫ«ΠΝΒΡ¥σ–ΓΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©CΓδGΓΈDNΘ°άμ”…ΦϊΫβΈωΘΜΘ®2Θ©–ΐΉΣΫ«ΠΝΒΡ¥σ–ΓΈΣ30ΓψΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©Ϋα¬έΘΚCΓδGΓΈDNΘ°œκΑλΖ®÷ΛΟςΓœDNC=ΓœCΓδGNΦ¥Ω…ΫβΨωΈ ΧβΘ°
Θ®2Θ©Ν§Ϋ”HCΓδΘ°÷ΛΟςΓςDCΓδH «Β»±Ώ»ΐΫ«–ΈΦ¥Ω…ΫβΨωΈ ΧβΘ°
Θ®1Θ©Ϋα¬έΘΚCΓδGΓΈDNΘ°
άμ”…ΘΚ»γΆΦ2÷–Θ§Ν§Ϋ”CΓδGΘ§DNΘ°
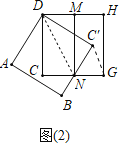
‘ΎRtΓςDCNΚΆRtΓςDCΓδN÷–ΘΚ
ΓΏDCΘΫDCΓδΘ§DNΘΫDNΘ§ΓœDCNΘΫΓœDCΓδNΘΫ90ΓψΘ§
ΓύRtΓςDCNΓ’RtΓςDCΓδNΘ®HLΘ©Θ©Θ§
ΓύCNΘΫCΓδNΘ§ΓœDNCΘΫΓœDNCΓδΘ§
”÷ΓΏCNΘΫNGΘ§
ΓύNGΘΫCΓδNΘ§
ΓύΓœNCΓδGΘΫΓœNGCΓδΘ§
”÷ΓΏΓœCNCΓδΘΫΓœNCΓδG+ΓœNGCΓδΘ§
ΓύΓœDNCΓδΘΫΓœNG CΓδΘ§
ΓύCΓδGΓΈDNΘ°
Θ®2Θ©Ν§Ϋ”HCΓδΘ°
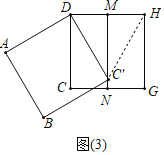
ΓΏΥΡ±Ώ–ΈDCGH «’ΐΖΫ–ΈΘ§ΒψMΘ§NΖ÷±π «DHΘ§CGΒΡ÷–ΒψΘ§
ΓύMN¥Ι÷±ΤΫΖ÷DHΘ§
ΓύDCΓδΘΫCΓδHΘ°
”÷ΓΏDHΘΫDCΓδΘ§
ΓύΓςDCΓδH «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύΓœCΓδDHΘΫ60ΓψΘ§
ΓύΓœCDCΓδΘΫ30ΓψΘ°
Γύ–ΐΉΣΫ«ΠΝΒΡ¥σ–ΓΈΣ30ΓψΘ°