题目内容
等腰△ABC的一个底角为30°,一条边长为 ,则△ABC的周长为________.
,则△ABC的周长为________.
6+4 或4+2
或4+2
分析:根据已知的边可以是腰长,也可以是底边的长度,然后作出底边上的高,再根据30°角所对的直角边等于斜边的一半,分别利用勾股定理进行求解即可.
解答: 解:如图,作AD⊥BC,D为垂足,则
解:如图,作AD⊥BC,D为垂足,则
BD=CD= AB(等腰三角形三线合一),
AB(等腰三角形三线合一),
①当已知边为腰长时,AB=2 ,∠B=30°,
,∠B=30°,
∴AD= AB=
AB= ,
,
在Rt△ABD中,BD=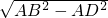 =
= =3,
=3,
∴BC=2BD=2×3=6,
∴△ABC的周长=6+2 ×2=6+4
×2=6+4 ,
,
②当已知边为底边时,BD= ×2
×2 =
= ,∠B=30°,
,∠B=30°,
在Rt△ABD中,AB2=AD2+BD2,
即AB2= AB2+
AB2+ 2,
2,
解得AB=2,
∴△ABC的周长=2×2+2 =4+2
=4+2 ,
,
综上所述,△ABC的周长为6+4 或4+2
或4+2 .
.
故答案为:6+4 或4+2
或4+2 .
.
点评:本题考查了等腰三角形的性质,直角三角形30°所对的直角边等于斜边的一半的性质,勾股定理,因为已知边不明确,要注意分情况进行讨论求解,避免漏解而导致出错.
 或4+2
或4+2
分析:根据已知的边可以是腰长,也可以是底边的长度,然后作出底边上的高,再根据30°角所对的直角边等于斜边的一半,分别利用勾股定理进行求解即可.
解答:
 解:如图,作AD⊥BC,D为垂足,则
解:如图,作AD⊥BC,D为垂足,则BD=CD=
 AB(等腰三角形三线合一),
AB(等腰三角形三线合一),①当已知边为腰长时,AB=2
 ,∠B=30°,
,∠B=30°,∴AD=
 AB=
AB= ,
,在Rt△ABD中,BD=
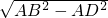 =
= =3,
=3,∴BC=2BD=2×3=6,
∴△ABC的周长=6+2
 ×2=6+4
×2=6+4 ,
,②当已知边为底边时,BD=
 ×2
×2 =
= ,∠B=30°,
,∠B=30°,在Rt△ABD中,AB2=AD2+BD2,
即AB2=
 AB2+
AB2+ 2,
2,解得AB=2,
∴△ABC的周长=2×2+2
 =4+2
=4+2 ,
,综上所述,△ABC的周长为6+4
 或4+2
或4+2 .
.故答案为:6+4
 或4+2
或4+2 .
.点评:本题考查了等腰三角形的性质,直角三角形30°所对的直角边等于斜边的一半的性质,勾股定理,因为已知边不明确,要注意分情况进行讨论求解,避免漏解而导致出错.

练习册系列答案
相关题目
 列要求画出图形.
列要求画出图形.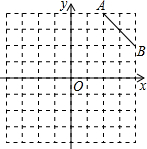 如图,已知A(2,4),B(4,2),C是第一象限内的一个格点(小正方形的顶点,叫格点),由点C与线段AB组成一个以AB为底,腰长为无理数的等腰三角形.
如图,已知A(2,4),B(4,2),C是第一象限内的一个格点(小正方形的顶点,叫格点),由点C与线段AB组成一个以AB为底,腰长为无理数的等腰三角形. 翻滚到有一个顶点与Q重合即停止滚动.
翻滚到有一个顶点与Q重合即停止滚动. 附加题:
附加题: 如图等腰△ABC的底边长为8cm,腰长为5cm,一个动点P在底边上从B向C以O.25cm/s的速度移动,请你探究,当P运动几秒时,P点与顶点A的连线PA与腰垂直.
如图等腰△ABC的底边长为8cm,腰长为5cm,一个动点P在底边上从B向C以O.25cm/s的速度移动,请你探究,当P运动几秒时,P点与顶点A的连线PA与腰垂直.