Question

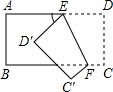如图1，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置上，∠EFB=67°，则∠AED′等于

1. A.
   53°
2. B.
   48°
3. C.
   46°
4. D.
   43°

Answer 1

C
分析：首先根据AD∥BC，求出∠FED的度数，然后根据轴对称的性质，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等，则可知∠DEF=∠FED′，最后求得∠AED′的大小．
解答：∵AD∥BC，
∴∠EFB=∠FED=67°，
由折叠的性质知，∠DEF=∠FED′=67°，
∴∠AED′=180°-2∠FED=180°-2×67°=46°．
故选C．
点评：本题考查的是翻折变换的性质及矩形的性质，熟知翻折变换的性质是解答此题的关键．