题目内容
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B、C、E在同一条直线上,连结DC.
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明: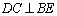 .
.
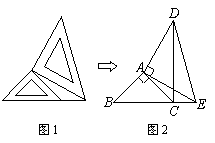
(1)解:△ABE ≌△ACD
证明:∵△ABC和△AED都是等腰直角三角形
∴AB=AC ,AE=AD, ∠ BAC= ∠EAD=90°.
∴∠BAC + ∠CAE = ∠EAD + ∠CAE
即∠BAE = ∠CAD -
∴△ABE≌△ACD
(2) ∵△ABE≌△ACD
∴∠B = ∠ACD
∵∠B+ ∠ACB =90°.
∴∠ACD+ ∠ACB= ∠BCD=90°. -
∴DC⊥BE

练习册系列答案
相关题目
小锦和小丽购买了价格分别相同的中性笔和笔芯,小锦买了20支笔和2盒笔芯,用了56元;小丽买了2支笔和3盒笔芯,仅用了28元.设每支中性笔x元和每盒笔芯y元,根据题意列方程组正确的是( )
|
| A. |
| B. |
|
|
| C. |
| D. |
|
抛物线 上部分点的横坐标x,纵坐标y的对应值如下表:
上部分点的横坐标x,纵坐标y的对应值如下表:
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中错误的是( )
A.抛物线与x轴的一个交点为(3,0) B.函数y=ax2+bx+c的最大值为6
C.抛物线的对称轴是直线x= D.在对称轴左侧,y随x增大而增大
D.在对称轴左侧,y随x增大而增大
在函数y= 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
|
| A. | x≥0 | B. | x>0 | C. | x≠0 | D. | x>0且x≠1 |






 是网格的一个顶点,以点
是网格的一个顶点,以点