题目内容
 23、
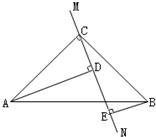
23、 在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.(1)当直线MN绕着点C旋转到如图所示的位置时,
求证:①△ADC≌△CEB; ②DE=AD+BE
(2)当直线MN绕着点C旋转到如图所示的位置时,①找出图中一对全等三角形;②DE、AD、BE之间有怎样的数量关系,并加以证明.
分析:(1)根据余角和补角的性质易证得∠DAC=∠ECB,已知∠ADC=∠CEB=90°,AC=CB,根据全等三角的判定AAS即可证明△ADC≌△CEB,根据各边的相等关系即可得DE=AD+BE.
(2)同理可证得△ADC≌△CEB,再根据各边的相等关系可得DE=AD-BE.
(2)同理可证得△ADC≌△CEB,再根据各边的相等关系可得DE=AD-BE.
解答:解:(1)∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=180°-90°=90°,
∴∠DAC=∠ECB;
在△ADC和△CEB中,∠ADC=∠CEB,∠DAC=∠ECB,AC=CB,
∴△ADC≌△CEB(AAS)①,(7分)
∴DC=EB,AD=CE,
∴DE=AD+BE.(9分)
(2)同理可得△ADC≌△CEB①;(11分)
∴AD=CE,CD=BE,
∴DE=AD-BE②.(14分)
∴∠ADC=∠CEB=90°,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=180°-90°=90°,
∴∠DAC=∠ECB;
在△ADC和△CEB中,∠ADC=∠CEB,∠DAC=∠ECB,AC=CB,
∴△ADC≌△CEB(AAS)①,(7分)
∴DC=EB,AD=CE,
∴DE=AD+BE.(9分)
(2)同理可得△ADC≌△CEB①;(11分)
∴AD=CE,CD=BE,
∴DE=AD-BE②.(14分)
点评:本题考查了全等三角形的判定和性质,涉及到补角和余角的性质,熟练掌握全等三角形的判定方法是解题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
在△ABC中,AC=8,BC=6,AB=10,则△ABC的外接圆半径长为( )
| A、10 | B、5 | C、6 | D、4 |
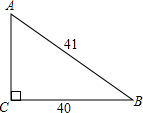 如图,在△ABC中,AC=
如图,在△ABC中,AC= 如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.
如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D. (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=