题目内容
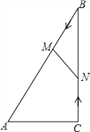
【题目】如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OD⊥AB于点O,分别交AC、CF于点E、D,且DE=DC.

(1)求证:CF是⊙O的切线;
(2)若⊙O的半径为5,BC=![]() ,求DE的长.
,求DE的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OC,欲证明CF是⊙O的切线,只要证明∠OCF=90°.
(2)作DH⊥AC于H,由△AEO∽△ABC,得![]() 求出AE,EC,再根据sin∠A=sin∠EDH,得到
求出AE,EC,再根据sin∠A=sin∠EDH,得到![]() ,求出DE即可.
,求出DE即可.
试题解析:连接OC,∵OA=OC,∴∠A=∠OCA,∵OD⊥AB,∴∠A+∠AEO=90°,∵DE=DC,∴∠DEC=∠DCE,∵∠AEO=∠DCE,∴∠AEO=∠DCE,∴∠OCE+∠DCE=90°,∠OCF=90°,∴OC⊥CF,∴CF是⊙O切线.
(2)作DH⊥AC于H,则∠EDH=∠A,∵DE=DC,∴EH=HC=![]() EC,∵⊙O的半径为5,BC=
EC,∵⊙O的半径为5,BC=![]() ,∴AB=10,AC=
,∴AB=10,AC=![]() ,∵△AEO∽△ABC,∴
,∵△AEO∽△ABC,∴![]() ,∴AE=
,∴AE=![]() ,∴EC=AC﹣AE=
,∴EC=AC﹣AE=![]() ,∴EH=
,∴EH=![]() EC=
EC=![]() ,∵∠EDH=∠A,∴sin∠A=sin∠EDH,∴
,∵∠EDH=∠A,∴sin∠A=sin∠EDH,∴![]() ,∴DE=
,∴DE=![]() =
= =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案【题目】已知y是x 的函数,自变量x的取值范围是x >0,下表是y与x 的几组对应值.
x | ··· | 1 | 2 | 3 | 5 | 7 | 9 | ··· |
y | ··· | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | ··· |
小腾根据学习一次函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为________;
②该函数的一条性质:__________________.