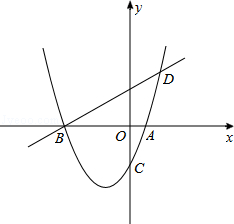题目内容
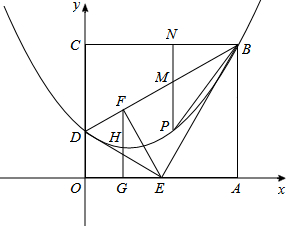
在平面直角坐标系中,已知M1(3,2),N1(5,﹣1),线段M1N1平移至线段MN处(注:M1与M,N1与N分别为对应点).

(1)若M(﹣2,5),请直接写出N点坐标.
(2)在(1)问的条件下,点N在抛物线 上,求该抛物线对应的函数解析式.
上,求该抛物线对应的函数解析式.
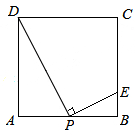
(3)在(2)问条件下,若抛物线顶点为B,与y轴交于点A,点E为线段AB中点,点C(0,m)是y轴负半轴上一动点,线段EC与线段BO相交于F,且OC:OF=2: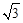 ,求m的值.
,求m的值.
(4)在(3)问条件下,动点P从B点出发,沿x轴正方向匀速运动,点P运动到什么位置时(即BP长为多少),将△ABP沿边PE折叠,△APE与△PBE重叠部分的面积恰好为此时的△ABP面积的 ,求此时BP的长度.
,求此时BP的长度.

(1)若M(﹣2,5),请直接写出N点坐标.
(2)在(1)问的条件下,点N在抛物线
 上,求该抛物线对应的函数解析式.
上,求该抛物线对应的函数解析式.(3)在(2)问条件下,若抛物线顶点为B,与y轴交于点A,点E为线段AB中点,点C(0,m)是y轴负半轴上一动点,线段EC与线段BO相交于F,且OC:OF=2:
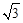 ,求m的值.
,求m的值.(4)在(3)问条件下,动点P从B点出发,沿x轴正方向匀速运动,点P运动到什么位置时(即BP长为多少),将△ABP沿边PE折叠,△APE与△PBE重叠部分的面积恰好为此时的△ABP面积的
 ,求此时BP的长度.
,求此时BP的长度.解:(1)(0,2)。
(2)∵N(0,2)在抛物线 上,∴k=2。
上,∴k=2。

∴抛物线的解析式为 。
。
(3)∵ ,
,
∴B( ,0)、A(0,2)、E(
,0)、A(0,2)、E( ,1)。
,1)。
∵CO:OF=2: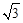 ,
,
∴CO=﹣m,FO= m,
m, 。
。
∵ ,∴
,∴ 。
。
整理得:m2+m=0。∴m=﹣1或0 。
∵m<0,∴m=﹣1。
(4)在Rt△ABO中, ,
,
∴∠ABO=30°,AB=2AO=4
①当∠BPE>∠APE时,连接A1B,则对折后如图2,A1为对折后A的所落点,△EHP是重叠部分。

∵E为AB中点,∴S△AEP=S△BEP= S△ABP。
S△ABP。
∵S△EHP= S△ABP,∴
S△ABP,∴ =S△EHP=S△BHP=
=S△EHP=S△BHP= S△ABP。
S△ABP。
∴A1H=HP,EH=HB=1。∴四边形A1BPE为平行四边形。
∴BP=A1E=AE=2。
②当∠BPE=∠APE时,重叠部分面积为△ABP面积的一半,不符合题意。
③当∠BPE<∠APE时.则对折后如图3,A1为对折后A的所落点,△EHP是重叠部分。

∵E为AB中点,∴S△AEP=S△BEP= S△ABP。
S△ABP。
∵S△EHP= S△ABP,∴S△EBH=S△EHP=
S△ABP,∴S△EBH=S△EHP= =
= S△ABP。
S△ABP。
∴BH=HP,EH=HA1=1。
又∵BE=EA=2,∴EH
 AP。∴AP=2。
AP。∴AP=2。
在△APB中,∠ABP=30°,AB=4,AP=2,
∴∠APB=90°。∴BP= 。
。
综上所述,BP=2或 。
。
(2)∵N(0,2)在抛物线
 上,∴k=2。
上,∴k=2。
∴抛物线的解析式为
 。
。(3)∵
 ,
,∴B(
 ,0)、A(0,2)、E(
,0)、A(0,2)、E( ,1)。
,1)。∵CO:OF=2:
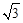 ,
,∴CO=﹣m,FO=
 m,
m, 。
。∵
 ,∴
,∴ 。
。整理得:m2+m=0。∴m=﹣1或0 。
∵m<0,∴m=﹣1。
(4)在Rt△ABO中,
 ,
,∴∠ABO=30°,AB=2AO=4
①当∠BPE>∠APE时,连接A1B,则对折后如图2,A1为对折后A的所落点,△EHP是重叠部分。

∵E为AB中点,∴S△AEP=S△BEP=
 S△ABP。
S△ABP。∵S△EHP=
 S△ABP,∴
S△ABP,∴ =S△EHP=S△BHP=
=S△EHP=S△BHP= S△ABP。
S△ABP。∴A1H=HP,EH=HB=1。∴四边形A1BPE为平行四边形。
∴BP=A1E=AE=2。
②当∠BPE=∠APE时,重叠部分面积为△ABP面积的一半,不符合题意。
③当∠BPE<∠APE时.则对折后如图3,A1为对折后A的所落点,△EHP是重叠部分。

∵E为AB中点,∴S△AEP=S△BEP=
 S△ABP。
S△ABP。∵S△EHP=
 S△ABP,∴S△EBH=S△EHP=
S△ABP,∴S△EBH=S△EHP= =
= S△ABP。
S△ABP。∴BH=HP,EH=HA1=1。
又∵BE=EA=2,∴EH

 AP。∴AP=2。
AP。∴AP=2。在△APB中,∠ABP=30°,AB=4,AP=2,
∴∠APB=90°。∴BP=
 。
。综上所述,BP=2或
 。
。试题分析:(1)首先根据点M的移动方向和单位得到点N的平移方向和单位,然后按照平移方向和单位进行移动即可:
由于图形平移过程中,对应点的平移规律相同,
由点M到点M′可知,点的横坐标减5,纵坐标加3,
故点N′的坐标为(5﹣5,﹣1+3),即(0,2)。
(2)将点N的坐标代入函数的解析式即可求得k值。
(3)配方后确定点B、A、E的坐标,根据CO:OF=2:
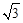 ,用m表示出线段CO、FO和BF的长,利用
,用m表示出线段CO、FO和BF的长,利用 得到关于m的方程,求得m的值即可。
得到关于m的方程,求得m的值即可。(4)分当∠BPE<∠APE时、当∠BPE=∠APE时、当∠BPE<∠APE时三种情况分类讨论即可。

练习册系列答案
相关题目
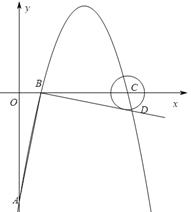

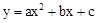 经过B,H, D三点,求抛物线解析式;
经过B,H, D三点,求抛物线解析式;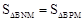 如果存在,求出点P的坐标;如果不存在,请说明理由.
如果存在,求出点P的坐标;如果不存在,请说明理由.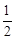 .
.