题目内容
9.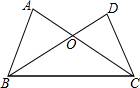 如图,下列条件不能证明△ABC≌△DCB的是( )
如图,下列条件不能证明△ABC≌△DCB的是( )| A. | AB=DC,AC=DB | B. | AB=DC,∠ABC=∠DCB | C. | BO=CO,∠A=∠D | D. | AC=BD,∠A=∠D |
分析 全等三角形的判定定理有SAS,ASA,AAS,SSS,根据以上内容逐个判断即可.
解答 解:A、AB=DC,AC=DB,BC=BC,符合全等三角形的判定定理“SSS”,即能推出△ABC≌△DCB,故本选项错误;
B、AB=DC,∠ABC=∠DCB,BC=BC,符合全等三角形的判定定理“SAS”,即能推出△ABC≌△DCB,故本选项错误;
C、在△AOB和△DOC中,
$\left\{\begin{array}{l}{∠AOB=∠DOC}\\{∠A=∠D}\\{OB=OC}\end{array}\right.$,
∴△AOB≌△DOC(AAS),
∴AB=DC,∠ABO=∠DCO,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠DCB,
在△ABC和△DCB中,
$\left\{\begin{array}{l}{AB=DC}\\{∠ABC=∠DCB}\\{BC=BC}\end{array}\right.$,
∴△ABC≌△DCB(SAS),
即能推出△ABC≌△DCB,故本选项错误;
D、具备条件AC=DB,BC=BC,∠A=∠D不能推出△ABC≌△DCB,故本选项正确.
故选D.
点评 本题考查了全等三角形的性质和判定的应用,能灵活运用全等三角形的判定定理进行推理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
相关题目
18.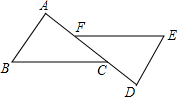 如图,AB∥DE,AF=DC,若要证明△ABC≌△DEF,还需补充的条件是( )
如图,AB∥DE,AF=DC,若要证明△ABC≌△DEF,还需补充的条件是( )
 如图,AB∥DE,AF=DC,若要证明△ABC≌△DEF,还需补充的条件是( )
如图,AB∥DE,AF=DC,若要证明△ABC≌△DEF,还需补充的条件是( )| A. | AC=DF | B. | AB=DE | C. | ∠A=∠D | D. | BC=EF |
19.方程3x2-4x-1=0的二次项系数和一次项系数分别为( )
| A. | 3和4 | B. | 3和-4 | C. | 3和-1 | D. | 3和1 |
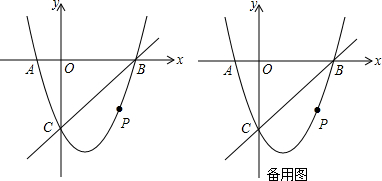
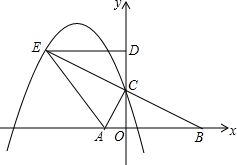 如图,在平面直角坐标系中,已知点A(-1,0)和点B(4,0),点C在y轴正半轴上,且∠ACB=90°,将△COB绕点C旋转180°得到△CDE,连结AE.
如图,在平面直角坐标系中,已知点A(-1,0)和点B(4,0),点C在y轴正半轴上,且∠ACB=90°,将△COB绕点C旋转180°得到△CDE,连结AE.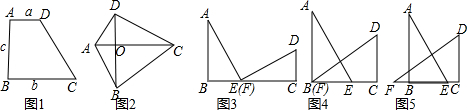
 如图,长方形ABCD的长与宽分别是6,4,建立适当的直角坐标系,写出各顶点的坐标.
如图,长方形ABCD的长与宽分别是6,4,建立适当的直角坐标系,写出各顶点的坐标.