题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动(
上运动(![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() ,作
,作![]() ,
,![]() 交线段
交线段![]() 于
于![]() .
.

![]() 点
点![]() 从
从![]() 向
向![]() 运动时,
运动时,![]() 逐渐变________(填“大”或“小”);设
逐渐变________(填“大”或“小”);设![]() ,
,![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 当
当![]() 的长度是多少时,
的长度是多少时,![]() ,请说明理由;
,请说明理由;
![]() 在点
在点![]() 的运动过程中,
的运动过程中,![]() 的形状也在改变,当
的形状也在改变,当![]() 等于多少度时,
等于多少度时,![]() 是等腰三角形?判断并说明理由.
是等腰三角形?判断并说明理由.
【答案】小
【解析】试题分析:![]() 利用三角形的内角和即可得出结论;
利用三角形的内角和即可得出结论;
![]() 当
当![]() 时,利用
时,利用![]() ,
,![]() ,求出
,求出![]() ,再利用
,再利用![]() ,即可得出
,即可得出![]() ;
;
![]() 由于
由于![]() 的形状是等腰三角形.分三种情况讨论计算.
的形状是等腰三角形.分三种情况讨论计算.
试题解析:![]() 在
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
当点![]() 从点
从点![]() 向
向![]() 运动时,
运动时,![]() 增大,
增大,
∴![]() 减小;
减小;
![]() 当
当![]() 时,
时,![]() ,
,
理由:∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
在![]() 和
和![]() 中
中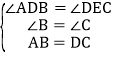 ,
,
∴![]() ;
;
![]() 当
当![]() 的度数为
的度数为![]() 或
或![]() 时,
时,![]() 的形状是等腰三角形,
的形状是等腰三角形,
理由:在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
①当![]() 时,
时,![]() ,
,
∴![]() ,不符合题意舍去,
,不符合题意舍去,
②当![]() 时,
时,![]() ,
,
根据三角形的内角和得,![]() ,
,
∴![]() ,
,
∴![]() ,
,
③当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的度数为
的度数为![]() 或
或![]() 时,
时,![]() 的形状是等腰三角形.
的形状是等腰三角形.

练习册系列答案
相关题目