题目内容
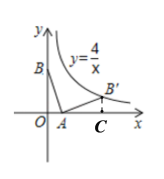
【题目】如图，在平面直角坐标系中线段AB的两个端点分别在坐标轴上，点A的坐标为（1，0），将线段AB绕点A顺时针旋转90°后，点B恰好落在反比例函数y＝
在第一象限内的分支上的点B′，则点B的坐标为（ ）
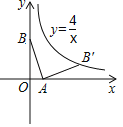
A.（0，2）B.（0，3）C.（0，4）D.（0，5）
【答案】B
【解析】
过点B′作
轴于C，根据旋转的性质、等角的余角相等、三角形全等的判定和性质，可以得到点B′的纵坐标，代入反比例函数解析式中，可以求得点B′的坐标，进而根据全等的性质得到
，可求得点B的坐标．
解：∵点A的坐标为（1，0），
∴
,
过点B′作轴于C，则
，
又∵由将线段AB绕点A顺时针旋转90°后得到AB′，可得
，
,
∴
，
，
∴
，
∴
≌
（AAS），
∴
，
,
∴点B′的纵坐标是1，
又∵当y＝1时，1＝
，
∴x＝4，
∴点B′的坐标是（4，1），
∴
，
∴，
∴点B的坐标是（0，3），
故选：B．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
