Question

【题目】某工厂加工一种商品，每天加工件数不超过100件时，每件成本80元，每天加工超过100件时，每多加工5件，成本下降2元，但每件成本不得低于70元.设工厂每天加工商品x（件），每件商品成本为y（元），

（1）求出每件成本y（元）与每天加工数量x（件）之间的函数关系式，并注明自变量的取值范围；

（2）若每件商品的利润定为成本的20%，求每天加工多少件商品时利润最大，最大利润是多少？

Answer 1

【答案】（1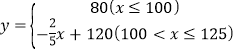）（2）每天加工125件时，利润最大，为1750元.

【解析】

（1）分两部分写函数解析式；

（2）设每天加工的利润为w元，当0＜x≤100时，w=20%×80x=16x，当100＜x≤125时，w=-（x-150）2+1800，结合函数图象求解.

（1）当时，；

∵

∴当时，，

∴

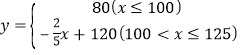
（2）设每天加工的利润为w元，

当时，，

∵，∴w随x的增大而增大，∴当时，w最大，最大值为1600元；

当时，

∵，开口向下，∴当时，w随x的增大而增大，

∵，∴当时，w最大，最大值为1750元，

∵1750>1600，∴当时，w最大.答：每天加工125件时，利润最大，为1750元.