题目内容
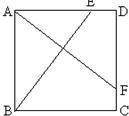24、如图，是一个正方形花园ACBD，E，F是它的两个门，且DE=CF，要修建两条路BE，AF，问这两条路长相等吗？它们有什么位置关系．分析：根据正方形的性质及全等三角形的判定SAS判定△BAE≌△ADF，从而得出BE=AF，再根据角与角之间的关系得出BE⊥AF．
解答：解：这两条路长相等且互相垂直
理由：∵四边形ACBD是正方形，
∴AB=AD=CD，∠BAD=∠D=90°，
∵DE=CF，
∴AD-DE=CD-CF，
即AE=DF，
∴△BAE≌△ADF（SAS），
∴BE=AF，∠ABE=∠DAE，
∵∠BAF+∠DAF=90°，
∴∠ABE+∠DAF=90°，
即BE⊥AF．
理由：∵四边形ACBD是正方形，
∴AB=AD=CD，∠BAD=∠D=90°，
∵DE=CF，
∴AD-DE=CD-CF，
即AE=DF，
∴△BAE≌△ADF（SAS），
∴BE=AF，∠ABE=∠DAE，
∵∠BAF+∠DAF=90°，
∴∠ABE+∠DAF=90°，
即BE⊥AF．
点评：此题考查了正方形的性质及全等三角形的判定，常用的全等三角形的判定有SSS，SAS，AAS，HL等．做题时要灵活运用．
练习册系列答案
轻松暑假总复习系列答案
相关题目
30、如图，是上海世博园内的一个矩形花园，花园长为100米，宽为50米，在它的四角各建有一个同样大小的正方形观光休息亭，四周建有与观光休息亭等宽的观光大道，其余部分（图中阴影部分）种植的是不同花草．已知种植花草部分的面积为3600米2，那么矩形花园各脚处的正方形观光休息亭的边长为多少米？
如图，是上海世博园内的一个矩形花园，花园长为100米，宽为50米，在它的四角各建有一个同样大小的正方形观光休息亭，四周建有与观光休息亭等宽的观光大道，其余部分（图中阴影部分）种植的是不同花草．已知种植花草部分的面积为3600米2，那么矩形花园各角处的正方形观光休息亭的边长为多少米？
