题目内容
【题目】已知二次函数
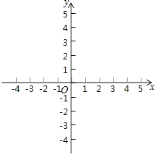
求出抛物线的对称轴和顶点坐标；
在直角坐标系中，直接画出抛物线（注意：关键点要准确，不必写出画图象的过程）；
根据图象回答：
①
取什么值时，抛物线在轴的上方？
②取什么值时，
的值随的值的增大而减小？
根据图象直接写出不等式
的解集．
【答案】（1）顶点坐标为：
，对称轴方程为：
；（2）图象见解析；（3）①当
或
时，图象位于
轴的上方；②当
时，图象位于轴的下方；
当
或
时，
．
【解析】
（1）先把抛物线
化为顶点式的形式，再求出其顶点坐标及对称轴方程即可；
（2）首先求得函数图象与坐标轴的交点坐标，然后做出图象即可；
（3）直接观察函数图象即可确定答案；
（4）直接观察图象即可确定答案.
解：
∵抛物线
可化为
的形式，
∴其顶点坐标为：，对称轴方程为：．
令
得：
或
，
所以与轴的交点坐标为
，
，
令
，解得：
，
所以与
轴的交点为
，
图象为：
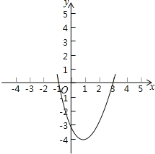
根据图象得：当或时，图象位于轴的上方；
当时，图象位于轴的下方；
根据图象得：当或时，．
练习册系列答案
阅读快车系列答案
相关题目
