题目内容
已知△ABC中,AB=5,AC=4,BC=3.E、F分别为AC、AB上的点.若△AEF与△ABC相似,且面积之比为1:4.则AE=________.
2或2.5
分析:由相似三角形的面积比等于相似比的平方求得△AEF与△ABC相似是 .分类讨论:①△AEF∽△ACB;②△AFE∽△ACB.由相似三角形的对应边成比例求得AE的长度.
.分类讨论:①△AEF∽△ACB;②△AFE∽△ACB.由相似三角形的对应边成比例求得AE的长度.
解答: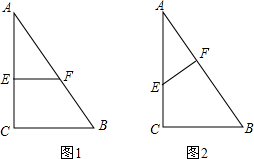 解:①如图1,当△AEF∽△ACB时,(
解:①如图1,当△AEF∽△ACB时,( )2=
)2=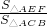 =
= ,即
,即 =
= ,
,
∵AC=4,
∴AE=2.
②如图2,当△AFE∽△ACB时,
( )2=
)2=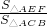 =
= ,即
,即 =
= ,
,
∵AB=5,
∴AE=2.5.
综上所述,AE的长度是2或2.5.
故答案是:2或2.5.
点评:本题考查了相似三角形的性质.此题在解答过程中,需要分类讨论,以防漏解.
分析:由相似三角形的面积比等于相似比的平方求得△AEF与△ABC相似是
 .分类讨论:①△AEF∽△ACB;②△AFE∽△ACB.由相似三角形的对应边成比例求得AE的长度.
.分类讨论:①△AEF∽△ACB;②△AFE∽△ACB.由相似三角形的对应边成比例求得AE的长度.解答:
 解:①如图1,当△AEF∽△ACB时,(
解:①如图1,当△AEF∽△ACB时,( )2=
)2=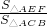 =
= ,即
,即 =
= ,
,∵AC=4,
∴AE=2.
②如图2,当△AFE∽△ACB时,
(
 )2=
)2=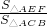 =
= ,即
,即 =
= ,
,∵AB=5,
∴AE=2.5.
综上所述,AE的长度是2或2.5.
故答案是:2或2.5.
点评:本题考查了相似三角形的性质.此题在解答过程中,需要分类讨论,以防漏解.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程证明△ABD≌△ACD的理由.
如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程证明△ABD≌△ACD的理由. 已知△ABC中,AB=AC,AD为BC边上的中线,BE为AC边上的高,
已知△ABC中,AB=AC,AD为BC边上的中线,BE为AC边上的高, 如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程,说明△ABD≌△ACD的理由.
如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程,说明△ABD≌△ACD的理由.
 如图:已知△ABC中,AB=17cm,BC=30cm,BC边上的中线AD=8cm.求证:△ABC是等腰三角形.
如图:已知△ABC中,AB=17cm,BC=30cm,BC边上的中线AD=8cm.求证:△ABC是等腰三角形.