题目内容
 如图,△OAB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,连接AC、BD.
如图,△OAB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,连接AC、BD.
求证:AC=BD.
证明:∵∠AOB=∠COD=90°,
∴∠AOC=∠BOD.
∵△OAB与△COD均为等腰三角形,
∴OA=OB,OC=OD.
在△AOC和△BOD中, ,
,
∴△AOC≌△BOD.
∴AC=BD.
分析:要证AC=BD,需证△AOC≌△BOD,由已知可证∠AOC=∠BOD,OA=OB,OC=OD,根据SAS即证得△AOC≌△BOD.
点评:本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等,本题是一道较为简单的题目.
∴∠AOC=∠BOD.
∵△OAB与△COD均为等腰三角形,
∴OA=OB,OC=OD.
在△AOC和△BOD中,
 ,
,∴△AOC≌△BOD.
∴AC=BD.
分析:要证AC=BD,需证△AOC≌△BOD,由已知可证∠AOC=∠BOD,OA=OB,OC=OD,根据SAS即证得△AOC≌△BOD.
点评:本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等,本题是一道较为简单的题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 6、如图,△OAB和△OCD是位似图形,则位似中心是
6、如图,△OAB和△OCD是位似图形,则位似中心是 如图,△OAB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,连接AC、BD.
如图,△OAB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,连接AC、BD.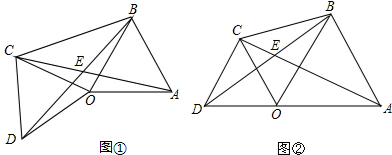
 如图,△OAB和△OA′B′,关于直线OP对称,则下列说法错误的是( )
如图,△OAB和△OA′B′,关于直线OP对称,则下列说法错误的是( ) 如图,△OAB和△OCD是位似图形,AB与CD平行吗?为什么?
如图,△OAB和△OCD是位似图形,AB与CD平行吗?为什么?