题目内容
直角三角形两直角边长分别是5和12,则它的三条中位线所围成的三角形的周长是________.
15
分析:先由勾股定理求得直角三角形的斜边的长度,然后由中点和中位线定义可得新三角形的各边长为原三角形各边长的一半,即可求其周长.
解答:∵直角三角形两直角边长分别是5和12,
∴该直角三角形的斜边长是: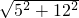 =13,
=13,
∴新三角形的各边长分别为:12÷2=6,5÷2=2.5,13÷2=6.5,
∴新三角形的周长=6+2.5+6.5=15.
故答案为15.
点评:本题考查了三角形中位线定理的应用、勾股定理的应用.解决本题的关键是利用中点定义和中位线定理得到新三角形各边长与原三角形各边长的数量关系.
分析:先由勾股定理求得直角三角形的斜边的长度,然后由中点和中位线定义可得新三角形的各边长为原三角形各边长的一半,即可求其周长.
解答:∵直角三角形两直角边长分别是5和12,
∴该直角三角形的斜边长是:
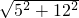 =13,
=13,∴新三角形的各边长分别为:12÷2=6,5÷2=2.5,13÷2=6.5,
∴新三角形的周长=6+2.5+6.5=15.
故答案为15.
点评:本题考查了三角形中位线定理的应用、勾股定理的应用.解决本题的关键是利用中点定义和中位线定理得到新三角形各边长与原三角形各边长的数量关系.

练习册系列答案
相关题目