题目内容
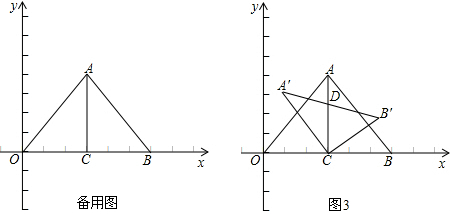
在平面直角坐标系中有两点A（-2，2），B（3，2），C是坐标轴上的一点，若△ABC是直角三角形，则满足条件的点共有
- A.1个
- B.2个
- C.4个
- D.6个
D
分析：因为A，B的纵坐标相等，所以AB∥x轴．因为C是坐标轴上的一点，所以过点A向x轴引垂线，过点B向x轴引垂线，分别可得一点，以AB为直径做圆可与坐标轴交于6点．所以满足条件的点共有6个．
解答：
解：∵A，B的纵坐标相等，
∴AB∥x轴，AB=3-（-2）=5．
∵C是坐标轴上的一点，过点A向x轴引垂线，可得一点，过点B向x轴引垂线，可得一点，以AB为直径作圆可与坐标轴交于4点．
∴根据直径所对的圆周角是90°，满足条件的点共有4个，为C，D，E，H．加上A、B共6个．
故选D．
点评：用到的知识点为：若△ABC是直角三角形，则它的任意一个顶点都有可能为直角顶点．
分析：因为A，B的纵坐标相等，所以AB∥x轴．因为C是坐标轴上的一点，所以过点A向x轴引垂线，过点B向x轴引垂线，分别可得一点，以AB为直径做圆可与坐标轴交于6点．所以满足条件的点共有6个．
解答：
解：∵A，B的纵坐标相等，∴AB∥x轴，AB=3-（-2）=5．
∵C是坐标轴上的一点，过点A向x轴引垂线，可得一点，过点B向x轴引垂线，可得一点，以AB为直径作圆可与坐标轴交于4点．
∴根据直径所对的圆周角是90°，满足条件的点共有4个，为C，D，E，H．加上A、B共6个．
故选D．
点评：用到的知识点为：若△ABC是直角三角形，则它的任意一个顶点都有可能为直角顶点．
练习册系列答案
相关题目
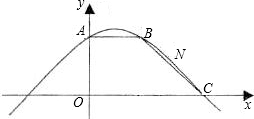在x轴上，过A、B、C三点的抛物线表达式为
