Question

在平面直角坐标系中，△AOC中，∠ACO=90^。把AO绕O点顺时针旋转90^。得OB，连接AB，作BD⊥直线CO于D，点A的坐标为（-3，1）

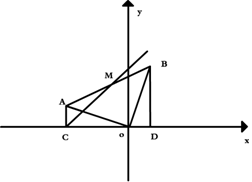
1.求直线AB的解析式

2.若AB中点为M，连接CM，动点P、Q分别从C点出发，点P沿射线CM以每秒√个单位长度的速度运动，点Q沿线段CD以每秒1个长度的速度向终点D运动，当Q点运动到D点时，P、Q同时停止，设△PQO的面积为S（S≠0）运动时间为T秒，求S与T的函数关系式，并直接写出自变量T的取值范围；

3.在（2）的条件下，动点P在运动过程中，是否存在P点，使四边形以P、O、B、N（N为平面上一点）为顶点的矩形，若存在求出T的值

 

Answer 1

 

1.∵∠AOB＝90°∴∠AOC+∠BOC＝90°

∵∠BOD＝90°∴∠OBD+∠BOD＝90°∴∠AOC=∠BOD

∵OA=OB    ∠AOC=∠BOD＝90°    ∴△AOC≌△OBD∴AC=OD    CO=BD

∵A(-3,1) ∴AC=OC=1,OC=BD=3         ∴B9(1,3) ∴y=x+

2.M(-1,2),C(-3,0) ∴lcm:y=x+3 

∴∠MOC=45°,过点P做PH⊥CO交CO于点H，S＝OQ，PH＝（3-t）×t=t+ t(0﹤t﹤3)

S=( t-3) t= t- t   (3﹤t≤4)

3.t₁= t ₂= t₃= t₄=2

解析:略