题目内容
(2012•江干区一模)如图,在平面直角坐标系中,点P从原点O出发,沿x轴向右以每秒一个单位 长的速度运动t秒(t>0),抛物线y=-x2+bx+c经过点O和点P.
长的速度运动t秒(t>0),抛物线y=-x2+bx+c经过点O和点P.
(1)求c,b(用t的代数式表示);
(2)抛物线y=-x2+bx+c与直线x=1和x=5分别交于M,N两点,当t>1时,
①在点P的运动过程中,你认为sin∠MPO的大小是否会变化?若变化,说明理由;若不变,求出sin∠MPO的值;
②△MPN的面积S与t的函数关系式;
③是否存在这样的t值,使得以O,M、N,P为顶点的四边形为梯形?如果存在,求出t的值;如果不存在,请说明理由.
 长的速度运动t秒(t>0),抛物线y=-x2+bx+c经过点O和点P.
长的速度运动t秒(t>0),抛物线y=-x2+bx+c经过点O和点P.(1)求c,b(用t的代数式表示);
(2)抛物线y=-x2+bx+c与直线x=1和x=5分别交于M,N两点,当t>1时,
①在点P的运动过程中,你认为sin∠MPO的大小是否会变化?若变化,说明理由;若不变,求出sin∠MPO的值;
②△MPN的面积S与t的函数关系式;
③是否存在这样的t值,使得以O,M、N,P为顶点的四边形为梯形?如果存在,求出t的值;如果不存在,请说明理由.
分析:(1)根据抛物线y=-x2+bx+c经过点O和点P,将O(0,0),P(t,0),代入求出c,b的值即可;
(2)①根据(1)中解析式得出M(1,t-1),得出AM=AP,∠PAM=45°即可得出sin∠MPO的大小不会变化;
②根据当1<t≤5时以及当t>5时,分别得出S△MPN=S△APM+S梯形ABNP-S△MBN,S△MPN=S梯形MABN+S△NBP-S△APM,求出即可;
③根据当MP∥ON时以及当MN∥OP时,分别得出t的值即可.
(2)①根据(1)中解析式得出M(1,t-1),得出AM=AP,∠PAM=45°即可得出sin∠MPO的大小不会变化;
②根据当1<t≤5时以及当t>5时,分别得出S△MPN=S△APM+S梯形ABNP-S△MBN,S△MPN=S梯形MABN+S△NBP-S△APM,求出即可;
③根据当MP∥ON时以及当MN∥OP时,分别得出t的值即可.
解答:解:(1)由题意得O(0,0),P(t,0),
代入y=-x2+bx+c,
得c=0,
-t2+bt=0,
即b=t.
即y=-x2+tx.
(2)当t>1时,①M(1,t-1),
即AM=t-1,AP=t-1,
即AM=AP,∠PAM=45°,sin∠MPO=sin45°=
是定值.
②当1<t≤5时,N(5,5t-25),
如图1,

过点N作AM的垂线,垂足为B,
S△MPN=S△APM+S梯形ABNP-S△MBN,
=
(t-1)2+
(t-1+4)×(25-5t)-
(t-1-5t+25)×4,
=-2t2+12t-10,
当t>5时,如图2,

S△MPN=S梯形MABN+S△NBP-S△APM,
=
(t-1+5t-25)×4+
(5t-25)(t-5)-
(t-1)2,
=2t2-12t+10,
③存在这样的t值,使得以O、M、N、P为顶点的四边形为梯形.
当MP∥ON时,如图3,

∵∠OPM=45°,∴∠PON=45°,
即N(5,-5),代入y=-x2+tx得-25+5t=-5.
解得t=4;
当MN∥OP时,如图4,

则M,N关于对称轴x=3对称,
即-
=3,
解得:t=6.
综上,当t=4或t=6时,以O、M、N、P为顶点的四边形为梯形.
代入y=-x2+bx+c,
得c=0,
-t2+bt=0,
即b=t.
即y=-x2+tx.
(2)当t>1时,①M(1,t-1),
即AM=t-1,AP=t-1,
即AM=AP,∠PAM=45°,sin∠MPO=sin45°=
| ||
| 2 |
②当1<t≤5时,N(5,5t-25),
如图1,

过点N作AM的垂线,垂足为B,
S△MPN=S△APM+S梯形ABNP-S△MBN,
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-2t2+12t-10,
当t>5时,如图2,

S△MPN=S梯形MABN+S△NBP-S△APM,
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=2t2-12t+10,
③存在这样的t值,使得以O、M、N、P为顶点的四边形为梯形.
当MP∥ON时,如图3,

∵∠OPM=45°,∴∠PON=45°,
即N(5,-5),代入y=-x2+tx得-25+5t=-5.
解得t=4;
当MN∥OP时,如图4,

则M,N关于对称轴x=3对称,
即-
| t |
| 2×(-1) |
解得:t=6.
综上,当t=4或t=6时,以O、M、N、P为顶点的四边形为梯形.
点评:此题主要考查了二次函数的综合应用以及梯形的判定和图形面积求法,正确利用数形结合进行分类讨论得出是解题关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
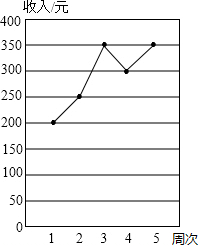 (2012•江干区一模)暑假里,小红参加了为期5周的勤工俭学活动,各周的收入情况如右图所示,以下结论中与右图反应的信息不相符的是( )
(2012•江干区一模)暑假里,小红参加了为期5周的勤工俭学活动,各周的收入情况如右图所示,以下结论中与右图反应的信息不相符的是( ) (2012•江干区一模)将矩形ABCD沿EF折叠,使点B与AD上的点B'重合,如BE=4,AB'=3,则BF的长为( )
(2012•江干区一模)将矩形ABCD沿EF折叠,使点B与AD上的点B'重合,如BE=4,AB'=3,则BF的长为( )