题目内容
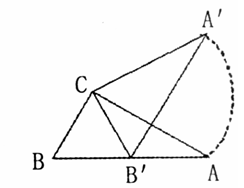
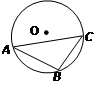
如图(3),在三角板△ABC中,∠ACB = 90℃,∠B = 60℃,BC = 1,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB延长线上时即停止转动,则点A转过的路径长为 .
|


考查有关圆的知识。
设A’B’与AC交于D点 ∵BC=B′C,且∠B=60°,
∴△BCB′是等边三角形, ∴∠BCB′=60°, ∵∠ACB = ∠A’CB’=90°
∴∠B′CA=90°-60°=30° ∵∠CB′D=∠B=60°,
∴∠CDB′=90° ∵∠A′CA=∠B′CA′-∠B′CA=90°-30°=60°,
∴∠CA’D=30°
∴B’D= B’C=
B’C= ×1=
×1= , ∴CD=
, ∴CD= =
= ∴A’C=2×
∴A’C=2× =
=
因为圆的弧长公式=2πr×圆心角度数÷360°
弧长AA’=
 。故答案是
。故答案是 。
。
设A’B’与AC交于D点 ∵BC=B′C,且∠B=60°,
∴△BCB′是等边三角形, ∴∠BCB′=60°, ∵∠ACB = ∠A’CB’=90°
∴∠B′CA=90°-60°=30° ∵∠CB′D=∠B=60°,
∴∠CDB′=90° ∵∠A′CA=∠B′CA′-∠B′CA=90°-30°=60°,
∴∠CA’D=30°
∴B’D=
 B’C=
B’C= ×1=
×1= , ∴CD=
, ∴CD= =
= ∴A’C=2×
∴A’C=2× =
=
因为圆的弧长公式=2πr×圆心角度数÷360°
弧长AA’=

 。故答案是
。故答案是 。
。
练习册系列答案
相关题目
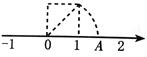
 中以点
中以点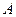 为圆心,
为圆心,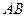 为半径作圆
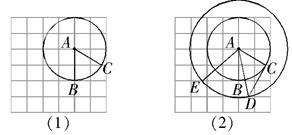
为半径作圆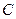 (如图(1)),过点
(如图(1)),过点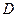 ,以点
,以点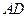 为半径作圆交网格于点
为半径作圆交网格于点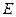
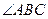 的度数;
的度数;
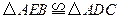 ;
;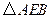 可以看作是由
可以看作是由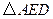 经过怎样的变换得到的?并判断
经过怎样的变换得到的?并判断 3),已知直线
3),已知直线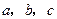 ,且a∥b,b∥c,在图中用
,且a∥b,b∥c,在图中用 直尺、三角板、圆规画等边三角形
直尺、三角板、圆规画等边三角形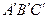 ,使三个顶点
,使三个顶点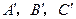 ,分别在直线
,分别在直线



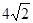
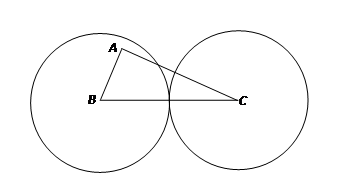
 2,求BC的值.
2,求BC的值.
