题目内容
△ABC中，AD是BC边上的中线，若AB=5，AC=9，则AD的取值范围是________．
2＜AD＜7
分析：延长AD到E，使AD=DE，可构造平行四边形ABEC，从而BE=AC，在△ABE中运用第三边的长度应是大于两边的差而小于两边的和，求得对角线AE的取值范围，从而得出AD的取值范围．
解答：
解：如图，延长AD到E，使AD=DE，
∵AD是BC边上的中线，∴BD=DC
∴四边形ABEC是平行四边形
∴BE=AC=9
在△ABE中，根据三角形的三边关系，得
9-5＜AE＜9+5，
即4＜AE＜14．
∵AD是BC边上的中线，
∴AD=
AE
∴AD的取值范围是2＜AD＜7．
故答案为：2＜AD＜7．
点评：本题需要理解的是如何根据已知的两条边求第三边的范围，灵活运用平行四边形的性质和三角形的三边关系是解题的关键．
分析：延长AD到E，使AD=DE，可构造平行四边形ABEC，从而BE=AC，在△ABE中运用第三边的长度应是大于两边的差而小于两边的和，求得对角线AE的取值范围，从而得出AD的取值范围．
解答：
解：如图，延长AD到E，使AD=DE，∵AD是BC边上的中线，∴BD=DC
∴四边形ABEC是平行四边形
∴BE=AC=9
在△ABE中，根据三角形的三边关系，得
9-5＜AE＜9+5，
即4＜AE＜14．
∵AD是BC边上的中线，
∴AD=
AE∴AD的取值范围是2＜AD＜7．
故答案为：2＜AD＜7．
点评：本题需要理解的是如何根据已知的两条边求第三边的范围，灵活运用平行四边形的性质和三角形的三边关系是解题的关键．
练习册系列答案
相关题目
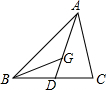如图，在△ABC中，AD是中线，G是重心，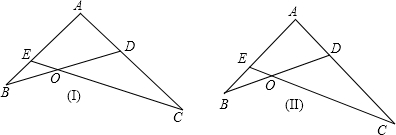
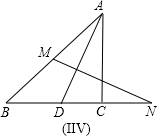
如图，在△ABC中，AD是BC边上的高，∠C=30°，AC=6，AB=4，求BD的长．（结果保留根号）
在直角△ABC中，AD是斜边上的高，角平分线CE交AD于O，过O引OF∥CB交AB于F．求证：AE=BF．