题目内容
如图,在直角坐标系中,点![]() 的坐标分别为
的坐标分别为![]() ,过
,过![]() 三点的抛物线的对称轴为直线
三点的抛物线的对称轴为直线![]() 为对称轴
为对称轴![]() 上一动点.
上一动点.
(1) 求抛物线的解析式;
(2) 求当![]() 最小时点
最小时点![]() 的坐标;
的坐标;
(3) 以点![]() 为圆心,以
为圆心,以![]() 为半径作
为半径作![]() .
.
①证明:当![]() 最小时,直线
最小时,直线![]() 与
与![]() 相切.
相切.
②写出直线![]() 与
与![]() 相切时,
相切时,![]() 点的另一个坐标:___________.
点的另一个坐标:___________.
 |
解:(1)设抛物线的解析式为![]() .
.
将![]() 代入上式,得
代入上式,得![]() .
.
解,得![]() .
.
![]() 抛物线的解析式为
抛物线的解析式为![]() .
.
即![]() .
.
(2)连接![]() ,交直线
,交直线![]() 于点
于点![]() .
.
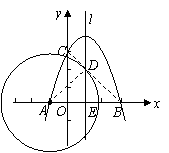 |
![]() 点
点![]() 与点
与点![]() 关于直线
关于直线 ![]() 对称,
对称,
![]() .
.
![]() .
.
由“两点之间,线段最短”的原理可知:
此时![]() 最小,点
最小,点![]() 的位置即为所求.
的位置即为所求.
设直线![]() 的解析式为
的解析式为![]() ,
,
由直线![]() 过点
过点![]() ,
,![]() ,得
,得![]()
解这个方程组,得![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
由(1)知:对称轴![]() 为
为![]() ,即
,即![]() .
.
将![]() 代入
代入![]() ,得
,得![]() .
.
![]() 点
点![]() 的坐标为(1,2).
的坐标为(1,2).
说明:用相似三角形或三角函数求点![]() 的坐标也可,答案正确给2分.
的坐标也可,答案正确给2分.
(3)①连接![]() .设直线
.设直线![]() 与
与![]() 轴的交点记为点
轴的交点记为点![]() .
.
由(1)知:当![]() 最小时,点
最小时,点![]() 的坐标为(1,2).
的坐标为(1,2).
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() 与
与![]() 相切.
相切.
②![]() .
.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: