题目内容
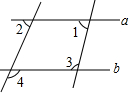如图，已知∠1和∠3互补，∠4=115°35′．求∠2的度数．分析：由∠1和∠3互补，根据同旁内角互补，两直线平行，即可证得a∥b，然后由两直线平行，同旁内角互补，即可证得：∠2+∠5=180°，继而求得∠2的度数．
解答：
解：∵∠1和∠3互补，
∴a∥b．（同旁内角互补，两直线平行），
∴∠2+∠5=180°．（两直线平行，同旁内角互补），
又∵∠5=∠4=115°35′，（对顶角相等），
∴∠2=180°-115°35′=64°25′．
解：∵∠1和∠3互补，∴a∥b．（同旁内角互补，两直线平行），
∴∠2+∠5=180°．（两直线平行，同旁内角互补），
又∵∠5=∠4=115°35′，（对顶角相等），
∴∠2=180°-115°35′=64°25′．
点评：此题考查了平行线的判定与性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
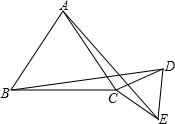如图，已知△ABC和△CDE都是等边三角形，问：线段AE、BD的长度有什么关系？请说明理由．
22、如图，已知△ABC和直线l，画出△ABC关于直线l的对称图形．
26、如图，已知△ABC和△AEF中，∠B=∠E，AB=AE，BC=EF，∠EAB=25°，∠F=57°；
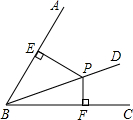如图，已知∠ABC和射线BD上一点P（点P与点B不重合），且点P到BA、BC的距离为PE、PF．