Question

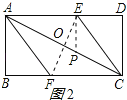
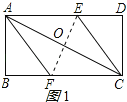
【题目】已知：如图所示的一张矩形纸片ABCD（AD＞AB），将纸片折叠一次，使点A与C重合，再展开，折痕EF交AD边于E，交BC边于F，分别连结AF和CE．

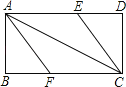
（1）求证：四边形AFCE是菱形；

（2）若AE＝13cm，△ABF的周长为30cm，求△ABF的面积；

（3）在线段AC上是否存在一点P，使得2AE2＝ACAP？若存在，请说明点P的位置，并予以证明；若不存在，请说明理由．

Answer 1

【答案】（1）见解析；（2）△ABF的面积＝30cm2；（3）存在，过E作EP⊥AD交AC于P，则P就是所求的点．理由见解析.

【解析】

（1）连结EF交AC于点O，由折叠的性质得出EF垂直平分AC，OA=OC，由矩形的性质得出∠B=90°，AD∥BC，得出∠EAO=∠FCO，由ASA证明△AOE≌△COF，得出OE=OF，证出四边形AFCE是平行四边形，即可得出结论；
（2）由菱形的性质得出AF=AE=13cm，设AB=xcm，BF=ycm，由勾股定理得出x2+y2=169①，由三角形的周长得出x+y=17cm，因此（x+y）2=289②，由①、②得出xy=60，△ABF的面积= AB×BF＝xy即可得出结果；
（3）过E作EP⊥AD交AC于P，则P就是所求的点．则∠AEP=90°，证出△AOE∽△AEP，得出对应边成比例，再由，即可得出结论．

证明：如图1所示,连结EF交AC于点O，当顶点A与C重合时，折痕EF垂直平分AC，

∴OA＝OC，

∵四边形ABCD是矩形，

∴∠B＝90°，AD∥BC，

∴∠EAO＝∠FCO，

在△AOE和△COF中，，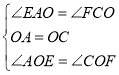

∴△AOE≌△COF（ASA），

∴OE＝OF，

∴四边形AFCE是平行四边形，

又∵EF⊥AC，

∴四边形AFCE是菱形；

（2）解：∵四边形AFCE是菱形，

∴AF＝AE＝13cm，

设AB＝xcm，BF＝ycm，

∵∠B＝90°，

∴x2+y2＝169 ①，

又∵△ABF的周长为30cm，

∴x+y+AF＝30cm，

∴x+y＝17cm，

∴（x+y）2＝289②，

由①、②得：xy＝60，

∴△ABF的面积＝AB×BF＝xy＝30（cm2）．

（3）解：存在，如图2，过E作EP⊥AD交AC于P，则P就是所求的点．理由如下：

由作法得：∠AEP＝90°，

由（1）得：∠AOE＝90°，

又∵∠EAO＝∠EAP，

∴△AOE∽△AEP，

∴，

∴AE2＝AOAP，

∵，

∴,

∴2AE2＝ACAP．