题目内容
(1999•武汉)已知,如图,OA是⊙O的半径,AB是以OA为直径的⊙O′的弦,O′B的延长线交⊙O于点C,且OA=4,∠OAB=45°.则由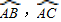 和线段BC所围成的图形面积是 .
和线段BC所围成的图形面积是 .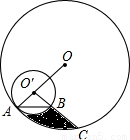
【答案】分析:根据∠OAB=45°可以发现CO′⊥OA.则阴影部分的面积等于直角三角形AO′C的面积减去扇形O′AB的面积.
连接OC、AC.根据线段垂直平分线的性质得到OC=OA,即可发现等边三角形AOC,从而求得∠A=60°.
解答: 解:连接OC、AC.
解:连接OC、AC.
∵O′A=O′B,∠OAB=45°,
∴∠AO′B=90°.
又OO′=AO′,
∴OC=AC.
又OA=OC,
∴△AOC是等边三角形.
∴∠A=60°.
∵O′A=2,
∴O′C=2 .
.
∴阴影部分的面积=S扇形OAC-S△OO'C-S扇形O'A0B= -2
-2 .
.
点评:注意发现此题中的等腰直角三角形和等边三角形.
连接OC、AC.根据线段垂直平分线的性质得到OC=OA,即可发现等边三角形AOC,从而求得∠A=60°.
解答:
 解:连接OC、AC.
解:连接OC、AC.∵O′A=O′B,∠OAB=45°,
∴∠AO′B=90°.
又OO′=AO′,
∴OC=AC.
又OA=OC,
∴△AOC是等边三角形.
∴∠A=60°.
∵O′A=2,
∴O′C=2
 .
.∴阴影部分的面积=S扇形OAC-S△OO'C-S扇形O'A0B=
 -2
-2 .
.点评:注意发现此题中的等腰直角三角形和等边三角形.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
 (x-1)2+2,则这条抛物线的顶点坐标是 .
(x-1)2+2,则这条抛物线的顶点坐标是 . x+2.又O1是x轴上一点,且⊙O1与直线AB切于点C,与y轴切于原点O.
x+2.又O1是x轴上一点,且⊙O1与直线AB切于点C,与y轴切于原点O.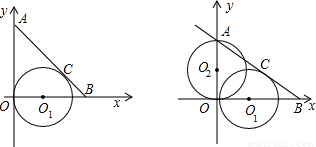
 x+2.又O1是x轴上一点,且⊙O1与直线AB切于点C,与y轴切于原点O.
x+2.又O1是x轴上一点,且⊙O1与直线AB切于点C,与y轴切于原点O.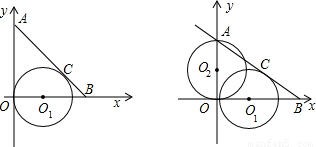
 (x-1)2+2,则这条抛物线的顶点坐标是 .
(x-1)2+2,则这条抛物线的顶点坐标是 .