题目内容
【题目】在平面直角坐标系中,二次函数y=ax2+2nx+c的图象过坐标原点.
(1)若a=-1.
①当函数自变量的取值范围是-1≤x≤2,且n≥2时,该函数的最大值是8,求n的值;
②当函数自变量的取值范围是![]() 时,设函数图象在变化过程中最高点的纵坐标为m,求m与n的函数关系式,并写出n的取值范围;
时,设函数图象在变化过程中最高点的纵坐标为m,求m与n的函数关系式,并写出n的取值范围;
(2)若二次函数的图象还过点A(-2,0),横、纵坐标都是整数的点叫做整点.已知点![]() ,二次函数图象与直线AB围城的区域(不含边界)为T,若区域T内恰有两个整点,直接写出a的取值范围.
,二次函数图象与直线AB围城的区域(不含边界)为T,若区域T内恰有两个整点,直接写出a的取值范围.
【答案】(1) ①n=3;② 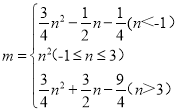 (2)
(2)![]()
【解析】
(1)①根据已知条件可确定抛物线图象的基本特征,从而列出关于![]() 的方程,即可得解;②根据二次函数图象的性质分三种情况进行分类讨论,从而得到
的方程,即可得解;②根据二次函数图象的性质分三种情况进行分类讨论,从而得到![]() 与
与![]() 的分段函数关系;
的分段函数关系;
(2)由![]() 得正负进行分类讨论,结合已知条件求得
得正负进行分类讨论,结合已知条件求得![]() 的取值范围.
的取值范围.
解:(1) ∵抛物线过坐标原点
∴c=0,a=-1
∴y=-x2+2nx
∴抛物线的对称轴为直线x=n,且n≥2,抛物线开口向下
∴当-1≤x≤2时,y随x的增大而增大
∴当x=2时,函数的最大值为8
∴-4+4n=8
∴n=3.
②若![]()
则![]()
∴抛物线开口向下,在对称轴右侧,![]() 随
随![]() 的增大而减小
的增大而减小
∴当![]() 时,函数值最大,
时,函数值最大,![]() ;
;
若![]()
则![]()
∴此时,抛物线的顶点为最高点
∴![]() ;
;
若![]()
则![]()
∴抛物线开口向下,在对称轴左侧,![]() 随
随![]() 的增大而增大
的增大而增大
∴当![]() 时,函数值最大,
时,函数值最大,![]()
∴综上所述: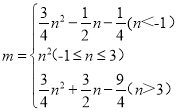
(2)结论:![]() 或
或![]()
证明:∵![]() 过
过![]()
∴![]()
∴![]()
①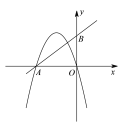
∵若![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,抛物线的对称轴为直线
,抛物线的对称轴为直线![]()
∴顶点为![]() ,对称轴与直线
,对称轴与直线![]() 交点坐标为
交点坐标为![]()
∴两个整点为![]() ,
,![]()
∵不含边界
∴![]()
∴![]()
②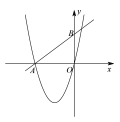
∵若![]() ,区域内已经确定有两个整点
,区域内已经确定有两个整点![]() ,
,![]()
∴在第三项象限和第一象限的区域内都要确保没有整点
∴![]()
∴![]()
∵当![]() 时,直线上的点的纵坐标为
时,直线上的点的纵坐标为![]() ,抛物线上的点的纵坐标为
,抛物线上的点的纵坐标为![]()
∴![]()
∴![]()
∴![]()
故答案为:(1)①![]() ;②
;②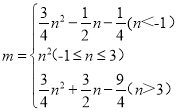 (2)
(2)![]() 或
或![]()

【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
| -1 | 0 | 1 | 3 |
| -3 | 1 | 3 | 1 |
下列结论:①抛物线的开口向下;②其图象的对称轴为![]() ;③当
;③当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而增大;④方程
的增大而增大;④方程![]() 有一个根大于4.其中正确的结论有( )
有一个根大于4.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个