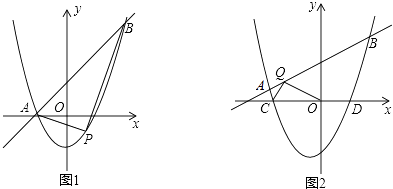题目内容
【题目】如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC. 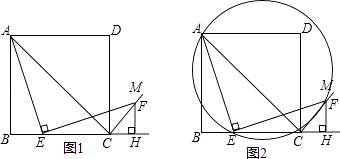
(1)试判断BE与FH的数量关系,并说明理由;
(2)求证:∠ACF=90°;
(3)连接AF,过A、E、F三点作圆,如图2,若EC=4,∠CEF=15°,求 ![]() 的长.
的长.
【答案】
(1)解:BE=FH.
证明:∵∠AEF=90°,∠ABC=90°,
∴∠HEF+∠AEB=90°,∠BAE+∠AEB=90°,
∴∠HEF=∠BAE,
在△ABE和△EHF中,
 ,
,
∴△ABE≌△EHF(AAS)
∴BE=FH
(2)解:由(1)得BE=FH,AB=EH,
∵BC=AB,
∴BE=CH,
∴CH=FH,
∴∠HCF=45°,
∵四边形ABCD是正方形,
∴∠ACB=45°,
∴∠ACF=180°﹣∠HCF﹣∠ACB=90°
(3)解:由(2)知∠HCF=45°,∴CF= ![]() FH.
FH.
∠CME=∠HCF﹣∠CEF=45°﹣15°=30°.
如图2,过点C作CP⊥EF于P,则CP= ![]() CF=
CF= ![]() FH.
FH.

∵∠CEP=∠FEH,∠CPE=∠FHE=90°,
∴△CPE∽△FHE.
∴ ![]() ,即
,即 ![]() ,
,
∴EF=4 ![]() .
.
∵△AEF为等腰直角三角形,∴AF=8.
取AF中点O,连接OE,则OE=OA=4,∠AOE=90°,
∴ ![]() 的弧长为:
的弧长为: ![]() =2π.
=2π.
【解析】(1)利用ABE≌△EHF求证BE=FH,(2)由BE=FH,AB=EH,推出CH=FH,得到∠HCF=45°,由四边形ABCD是正方形,所以∠ACB=45°,得出∠ACF=90°,(3)作CP⊥EF于P,利用相似三角形△CPE∽△FHE,求出EF,利用公式求出 ![]() 的长.
的长.

【题目】为了了解学校开展“孝敬父母,从家务劳动做起”活动的实施情况,该校抽取八年级![]() 名学生,调查他们一周(按七天计算)做家务所用时间(单位:小时)得到一组数据,绘制成下表:
名学生,调查他们一周(按七天计算)做家务所用时间(单位:小时)得到一组数据,绘制成下表:
时间 | 划记 | 人数 | 所占百分比 |
|
|
|
|
| 正正正 |
|
|
| 正正 |
| |
| 正 |
|
|
| 正 |
|
|
| 正 |
| |
| 正 |
| |
合计 |
|
|
(1)请填表中未完成的部分;
(2)根据以上信息判断,每周做家务的时间不超过![]() 小时的学生所占的百分比是多少?
小时的学生所占的百分比是多少?
(3)针对以上情况,写出一个20字以内的倡导“孝敬父母,热爱劳动”的句子.