题目内容
已知M和N表示单项式，且满足2x（M+3x）=6x2y2+N，则M= ，N= ．
考点：单项式乘多项式
专题：
分析：利用单项式乘以多项式运算法则求出即可．
解答：解：∵2x（M+3x）=6x2y2+N，
∴2xM+6x2=6x2y2+N，
则N=6x2，M=6x2y2÷2x=3xy2，
故答案为：3xy2，6x2．
∴2xM+6x2=6x2y2+N，
则N=6x2，M=6x2y2÷2x=3xy2，
故答案为：3xy2，6x2．
点评：此题主要考查了单项式乘多项式，正确掌握运算法则是解题关键．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
如图，AD是△ABC的高，AC=12cm，∠BAD=30°，∠DAC=45°．求AB的长．若3（x+1）2-48=0，则x的值等于（ ）
| A、±4 | B、3或-5 |
| C、-3或5 | D、3或5 |
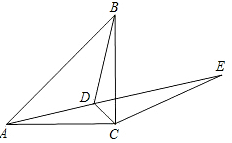如图，在△ABC中，∠ACB=90°，AC=BC，点D为△ABC内一点，∠CAD=∠CBD=15°，点E为AD延长线上的一点，且CE=AC．