题目内容
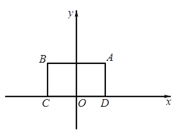
【题目】对于⊙P及一个矩形给出如下定义:如果⊙P上存在到此矩形四个顶点距离都相等的点,那么称⊙P是该矩形的“等距圆”.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A的坐标为(![]() ,
,![]() ),顶点C、D在x轴上,且OC=OD.
),顶点C、D在x轴上,且OC=OD.
(1)当⊙P的半径为4时,
①在P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() )中可以成为矩形ABCD的“等距圆”的圆心的是 ;
)中可以成为矩形ABCD的“等距圆”的圆心的是 ;
②如果点P在直线![]() 上,且⊙P是矩形ABCD的“等距圆”,求点P的坐标;
上,且⊙P是矩形ABCD的“等距圆”,求点P的坐标;
(2)已知点P在![]() 轴上,且⊙P是矩形ABCD的“等距圆”,如果⊙P与直线AD没有公共点,直接写出点P的纵坐标m的取值范围.
轴上,且⊙P是矩形ABCD的“等距圆”,如果⊙P与直线AD没有公共点,直接写出点P的纵坐标m的取值范围.
【答案】(1) ①![]() ; ②
; ②![]()
![]() 或
或![]()
(2)![]()
【解析】分析:(1)①由点A的坐标为(![]() ,2),顶点C、D在x轴上,且OC=OD,可求得点B,C,D的坐标,继而可求得到此矩形四个顶点距离都相等的点E的坐标,然后由⊙P的半径为4,即可求得答案;
,2),顶点C、D在x轴上,且OC=OD,可求得点B,C,D的坐标,继而可求得到此矩形四个顶点距离都相等的点E的坐标,然后由⊙P的半径为4,即可求得答案;
②首先设P的坐标为(x,-![]() x+1),易得x2+(-
x+1),易得x2+(-![]() x+1-1)2=42,继而求得答案;
x+1-1)2=42,继而求得答案;
(2)由题意可得|m-1|<![]() ,且|m-1|≠0,继而求得答案.
,且|m-1|≠0,继而求得答案.
详解:(1)∵点A的坐标为(![]() ,2),顶点C、D在x轴上,且OC=OD,
,2),顶点C、D在x轴上,且OC=OD,
∴点B的坐标为(-![]() ,2),点C的坐标为(-
,2),点C的坐标为(-![]() ,0),点D的坐标为(
,0),点D的坐标为(![]() ,0),
,0),
∴矩形ABCD的中心E的坐标为(0,1),
当⊙P的半径为4时,
①若P1(0,-3),则PE=1+3=4,
若P2(2![]() ,3),则PE=
,3),则PE=![]() =4,
=4,
若P3(-2![]() ,1)则PE=
,1)则PE=![]() ,
,
∴可以成为矩形ABCD的“等距圆”的圆心的是:P1(0,-3),P2(2![]() ,3);
,3);
故答案为:P1(0,-3),P2(2![]() ,3).
,3).

②∵设P的坐标为(x,-![]() x+1),
x+1),
∵E为(0,1),
∴x2+(-![]() x+1-1)2=42,
x+1-1)2=42,
解得:x=±2![]() ,
,
当x=2![]() 时,y=-
时,y=-![]() ×2
×2![]() +1=-1;
+1=-1;
当x=-2![]() 时,y=-
时,y=-![]() ×(-2
×(-2![]() )+1=3;
)+1=3;
∴点P的坐标为(2![]() ,-1)或(-2
,-1)或(-2![]() ,3);
,3);
(2)∵点P在y上,且⊙P是矩形ABCD的“等距圆”,且⊙P与直线AD没有公共点,
∴|m-1|<![]() ,且|m-1|≠0,
,且|m-1|≠0,
解得:1-![]() <m<1+
<m<1+![]() 且m≠1.
且m≠1.
∴点P的纵坐标m的取值范围为:1-![]() <m<1+
<m<1+![]() 且m≠1.
且m≠1.

 教材全解字词句篇系列答案
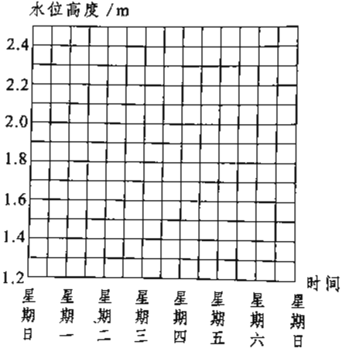
教材全解字词句篇系列答案【题目】下表是一个水文站在雨季对某条河一周内水位变化情况的记录.其中,水位上升用正数表示,水位下降用负数表示(水位变化的单位:m).
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
变化 | +0.4 | -0.3 | -0.4 | -0.3 | +0.2 | +0.2 | +0.1 |
注:①表中记录的数据为每天12时的水位与前一天12时的水位的变化量.
②上周日12时的水位高度为2m.
(1)请你通过计算说明本周末水位是上升了还是下降了;
(2)用折线图表示本周每天的水位,并根据折线图说明水位在本周内的升降趋势.