题目内容
四边形ABCD中，对角线AC、BD交于点O，若OA=OB=OC=OD，则这个四边形是________．
矩形
分析：根据OA=OB=OC=OD，判断四边形ABCD是平行四边形．然后根据AC=BD，判定四边形ABCD是矩形．
解答：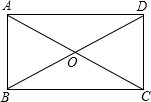
解：∵对角线AC、BD交于点O，OA=OB=OC=OD，
∴四边形ABCD是平行四边形，
又∵OA+OC=OD+OB
即AC=BD
∴四边形ABCD是矩形．
故答案为：矩形．
点评：本题是考查矩形的判定方法，常见的又3种：
（1）一个角是直角的四边形是矩形；
（2）三个角是直角的四边形是矩形；
（3）对角线相等的平行四边形是矩形．
分析：根据OA=OB=OC=OD，判断四边形ABCD是平行四边形．然后根据AC=BD，判定四边形ABCD是矩形．
解答：
解：∵对角线AC、BD交于点O，OA=OB=OC=OD，∴四边形ABCD是平行四边形，
又∵OA+OC=OD+OB
即AC=BD
∴四边形ABCD是矩形．
故答案为：矩形．
点评：本题是考查矩形的判定方法，常见的又3种：
（1）一个角是直角的四边形是矩形；
（2）三个角是直角的四边形是矩形；
（3）对角线相等的平行四边形是矩形．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
5、如图，平行四边形ABCD中，对角线AC，BD相交于点O，则图中成中心对称的三角形共有（ ）
1、如图，在四边形ABCD中，AB∥CD，AD∥BC，AC，BD相交于O，则图中能够全等的三角形共有（ ）对．
21、已知在四边形ABCD中，∠A=∠C，∠B=∠D．求证：四边形ABCD是平行四边形．
，命题的结论：四边形ABCD是平行四边形，请写一个真命题和一个假命题．