题目内容
 如图,BA⊥AC于A,DE⊥AC于E,AB=DE,AE=CF,试说明:∠D=∠B.
如图,BA⊥AC于A,DE⊥AC于E,AB=DE,AE=CF,试说明:∠D=∠B.
分析:本题可转化为证明△ABC≌△EDF,首先根据BA⊥AC,DE⊥AC得出∠A=∠DEF=90°,然后根据AE=CF得出AC=EF,结合AB=DE利用SAS判定定理可得出结论.
解答:解:∵BA⊥AC,DE⊥AC,
∴∠A=∠DEF=90°,
∵AE=CF,
∴AC=EF,
在△ABC与△EDF中,
,
∴△ABC≌△EDF(SAS),
∴∠D=∠B.
∴∠A=∠DEF=90°,
∵AE=CF,
∴AC=EF,
在△ABC与△EDF中,
|
∴△ABC≌△EDF(SAS),
∴∠D=∠B.
点评:本题主要考查全等三角形的判定及性质,注意掌握①判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL;②全等三角形的对应边对应角分别相等.

练习册系列答案
相关题目


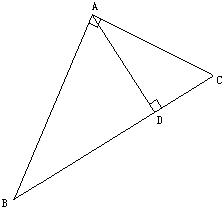
 如图,BA⊥AC于A,DE⊥AC于E,AB=DE,AE=CF,试说明:∠D=∠B.
如图,BA⊥AC于A,DE⊥AC于E,AB=DE,AE=CF,试说明:∠D=∠B.