题目内容
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
【小题1】(1)设AE=x,四边形AMND的面积
 为 S,求 S关于x 的函数解析式,并指明该函数的定义域;
为 S,求 S关于x 的函数解析式,并指明该函数的定义域;【小题2】(2)当AM为何值时,四边形AMND的面积最大?最大值是多少?
【小题3】(3)点M能是AB边上任意一点吗?请求出AM的取值范围.
【小题1】⑴依题意,点B和E关于MN对称,则ME=MB=4-AM.
再由AM2+AE2=ME2=(4-AM)2,得AM=2-
 . ……………………1分
. ……………………1分作MF⊥DN于F,则MF=AB,且∠BMF=90°.
∵MN⊥BE,∴∠ABE= 90°-∠BMN.
又∵∠FMN =∠BMF -∠BMN=90°-∠BMN,
∴∠FMN=∠ABE.
∴Rt△FMN≌Rt△ABE.
 ∴FN=AE=x,DN=DF+FN=AM+x=2-
∴FN=AE=x,DN=DF+FN=AM+x=2- +x. ………………………2分
+x. ………………………2分∴S=
 (AM+DN)×AD
(AM+DN)×AD=(2-
 +
+ )×4
)×4= -
 +2x+8. ……………………………3分
+2x+8. ……………………………3分其中,0≤x<4.
【小题2】⑵∵S= -
 +2x+8= -
+2x+8= - (x-2)2+10,
(x-2)2+10,∴当x=2时,S最大=10; …………………………………………5分
此时,AM=2-
 ×22="1.5 " ………………………………………6分
×22="1.5 " ………………………………………6分答:当AM=1.5时,四边形AMND的面积最大,为10
【小题3】⑶不能,0<AM≤2.解析:
略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 22、如图,方格纸中每个小正方形的边长都是单位1.
22、如图,方格纸中每个小正方形的边长都是单位1.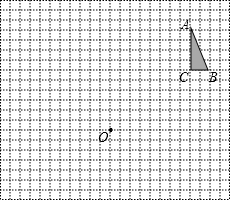 如图,方格纸中每个小正方形的边长都是单位1.
如图,方格纸中每个小正方形的边长都是单位1.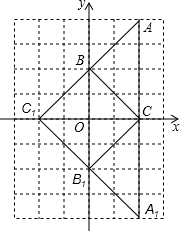 如图,方格纸中的每个小方格都是边长为1个单位的正方形.已知△ABC的顶点均在格点上,建立直角坐标系后,点A的坐标为(2,4).
如图,方格纸中的每个小方格都是边长为1个单位的正方形.已知△ABC的顶点均在格点上,建立直角坐标系后,点A的坐标为(2,4). 轴的对称点得到C点,最后做点C关于
轴的对称点得到C点,最后做点C关于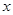 轴的对称点得到D点。
轴的对称点得到D点。

 重合,画出平移后的三角形.
重合,画出平移后的三角形. ,画出旋转后的图形.
,画出旋转后的图形.