Question

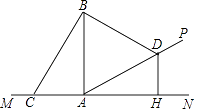
【题目】如图1，在矩形ABCD中，动点E从A出发，沿AB→BC方向运动，当点E到达点C时停止运动，过点E做FE⊥AE，交CD于F点，设点E运动路程为x，FC=y，如图2所表示的是y与x的函数关系的大致图象，当点E在BC上运动时，FC的最大长度是 ，则矩形ABCD的面积是（ ）

A.
B.5
C.6
D.

Answer 1

【答案】B
【解析】解：若点E在BC上时，如图

∵∠EFC+∠AEB=90°，∠FEC+∠EFC=90°，
∴∠CFE=∠AEB，∵在△CFE和△BEA中， ，∴△CFE∽△BEA，
由二次函数图象对称性可得E在BC中点时，CF有最大值，此时 = ，BE=CE=x﹣ ，即 ，
∴y= ，当y= 时，代入方程式解得：x1= （舍去），x2= ，
∴BE=CE=1，∴BC=2，AB= ，
∴矩形ABCD的面积为2× =5；
故选B．
【考点精析】关于本题考查的函数的图象，需要了解函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值才能得出正确答案．