Question

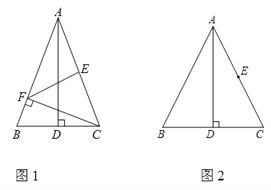
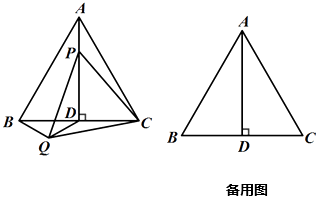
【题目】如图，正△ABC 中，高线 ，点 从点 出发，沿着 运动到点 停止，以 为边向左下方作正 ，连接 ， .

（1）求证： ≌ ；
（2）在点P的运动过程中，当 是等腰三角形时，求 的度数；
（3）直接写出在点 P的运动过程中， 的最小值.

Answer 1

【答案】
（1）

证明：∵ABC和PQC是正三角形，∴AC=BC，PC=QC，ACB=PCQ=60，

又∵ACP=60-BCP，BCP=60-BCP，∴ACP=BCP.

在ACP和BCQ中，

∵,

∴ACPBCQ（SAS）.

（2）

解：由（1）知，ACPBCQ，∴QBD=PAC=30，

当ΔBDQ 是等腰三角形时，

①若BQ=QD，,如图1，则BDQ=30；

图1

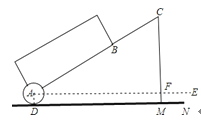
②若BQ=BD，如图2，则BDQ=75；

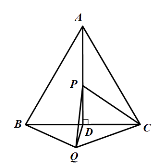
图2

③若BD=DQ，如图3，则BDQ=120.

图3

答：BDQ的度数为30或75或120.

（3）

【解析】（3）解：如图4，过点P作PMAB于点M，

图4
∵BAD=30，PM=AP，即：AP=2PM，
∴AP+2PC=2PM+2PC=2（PM+PC），
∴当AP+2PC最小时，即2PM+2PC最小，即PM+PC最小. ∴当点P运动到P、C、M在同一直线上时，PM+PC最小.
过点C作CNAB于点N，
当点P运动到CN与AD的交点处时，PM+PC最小，最小值为等边三角形ABC的高CN=6，
∴AP+2PC的最小值=26=12.
【考点精析】利用等腰三角形的性质和轴对称-最短路线问题对题目进行判断即可得到答案，需要熟知等腰三角形的两个底角相等（简称：等边对等角）；已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径．