题目内容
如图,已知直线AB与 轴交于点C,与双曲线
轴交于点C,与双曲线 交于A(3,
交于A(3, )、B(-5,
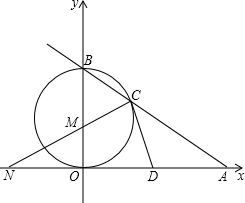
)、B(-5,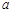 )两点.AD⊥
)两点.AD⊥ 轴于点D,BE∥
轴于点D,BE∥ 轴且与
轴且与 轴交于点E.
轴交于点E.
(1)求点B的坐标及直线AB的解析式;
(2)判断四边形CBED的形状,并说明理由.
(1)∵双曲线 过A(3,
过A(3, ),∴
),∴ .把B(-5,
.把B(-5,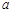 )代入
)代入 ,
,
得 . ∴点B的坐标是(-5,-4).
. ∴点B的坐标是(-5,-4).
设直线AB的解析式为 ,
,
将 A(3, )、B(-5,-4)代入得,
)、B(-5,-4)代入得, , 解得:
, 解得: .
.
∴直线AB的解析式为: .
.
(2)四边形CBED是菱形.理由如下:
点D的坐标是(3,0),点C的坐标是(-2,0).
∵ BE∥ 轴, ∴点E的坐标是(0,-4).
轴, ∴点E的坐标是(0,-4).
而CD =5, BE=5, 且BE∥CD.
∴四边形CBED是平行四边形.
在Rt△OED中,ED2=OE2+OD2, ∴ ED= =5,∴ED=CD.
=5,∴ED=CD.
∴□CBED是菱形.
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM.
方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM.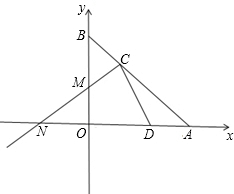 如图,已知直线AB与x轴、y轴分别交于A和B,OA=4,且OA、OB长是关于x的方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM并延长交x轴于N.
如图,已知直线AB与x轴、y轴分别交于A和B,OA=4,且OA、OB长是关于x的方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM并延长交x轴于N. 26、如图,已知直线AB与CD相交于点O,OB平分∠EOD,∠1+∠2=90°,
26、如图,已知直线AB与CD相交于点O,OB平分∠EOD,∠1+∠2=90°, A=3,点C的横坐标为-3,tan∠BAO=
A=3,点C的横坐标为-3,tan∠BAO= 如图,已知直线AB与CD相交于点O,OE⊥CD,OF平分∠BOE,若∠AOC=∠EOF,
如图,已知直线AB与CD相交于点O,OE⊥CD,OF平分∠BOE,若∠AOC=∠EOF,